5.2. El cono: área y volumen
El cono tampoco es una figura desconocida, seguramente porque podemos ver conos normalmente en nuestra vida cotidiana. Como ves en las imágenes podemos encontrar conos en la carretera o en una heladería.
 |
.jpg "cucurucho en forma de cono") |
| http://www.tecnosports.com bajo licencia de creative commons |
http://modaestiloytendencias.blogspot.com/ bajo licencia de creative commons |
Vamos a obtener el área y el volumen del cono, y posteriormente vamos a hacer algún ejemplo. Para ello vamos a ver un cono con los elementos que necesitamos para poder utilizar éstas fórmulas.
Vemos el cono que tiene tres elementos esenciales: r, el radio del circulo que es su base; a, la altura del cono; y g, que es la generatriz del cono. Recibe este nombre tan raro, porque si coges un palito (una pajita de las de beber por ejemplo) y la mueves en el aire, estás formando en el aire un cono, o sea, creas o generas un cono, de ahí que se llame, generatriz del cono.
Actividad
La expresión del área es:
ÁREA DE UN CONO: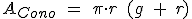 
; donde g es el lado o generatriz del cono, y r el radio del circulo que es la base del cono.
Y la del volumen:
VOLUMEN DE UN CONO: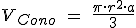 
; donde a es la altura del cono.
Como ejemplo, vamos a calcular el área y el volumen del cono que tiene las siguiente medidas: g = 15 cm, a = 12 cm, y r = 9 cm.
Calculamos el área: 
;
y el volumen: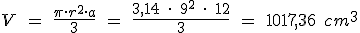 
Si tuviéramos un cucurucho para rellenar de nata, a ras, o sea, que no sobresalga helado del cucurucho; y ese cucurucho tuviera las siguientes dimensiones: el radio de la base mide 3 cm; la altura del cucurucho mide 15 cm; y la generatriz del cucurucho mide 17 cm, qué área de galleta ha sido utilizada en la fabricación del cucurucho, y y qué volumen de helado de nata se ha utilizado para rellenar el cucucucho.
Para calcular el área tendremos que tener en cuenta que el cucurucho no está tapado, luego tendremos que restar el área del circulo, una vez obtenido el valor del área del cono. Vamos a calcular el área del cono:
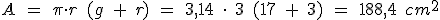
y a esto hay que restarle el área del circulo, que es:
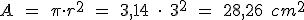
así restando tenemos: A = 188,4 - 28,26 = 160,14 cm2
Para el volumen de helado de nata, no hay ninguna cuestión a tener en cuenta:
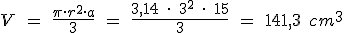
Caso de estudio
Antiguamente, para salir en un paso de Semana Santa, el penitente tenía que hacerse su propio capirote. Uno cogía una cartulina y se lo fabricaba artesanalmente. Vamos a fabricarnos uno con nuestra imaginación. Medimos el diametro de nuestra cabeza, y obtenemos 18 cm allí donde debe apoyar el capirote. Medimos la altura que debe tener el capirote, y nos sale 45 cm, y aunque no lo necesitamos para construirlo medimos también su generatriz, que vale 48 cm. Calcula el área de cartulina que necesitamos para hacer el capirote.
 |
| http://elpenitenteonubense.blogspot.com bajo licencia de creative commons |
