4. Área y volumen de una pirámide cuadrángular
Vamos a conseguir las fórmulas del área y del volumen de una pirámide cuadrangular, que llamaremos por comodidad a partir de ahora, simplemente pirámide.
Como el área es la suma de todas las áreas de los polígonos que la forman, será la suma del área de la base, y la suma de las áreas de los cuatro triángulos.
El área de la base es sencilla, puesto que vale la base al cuadrado. Para el área de los cuatro triángulos vamos a utilizar la expresión siguiente:
ÁREA DE LAS CARAS LATERALES:
; con lo cual la expresión final del área de una pirámide será:
Actividad
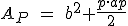; donde b es el valor del lado de la base, p es el perímetro de la base y ap es la apotema.
Para el volumen la expresión es la siguiente:
VOLUMEN DE LA PIRÁMIDE CUADRANGULAR: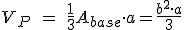 
; donde a es la altura de la pirámide.
Veamos un ejemplo:
Si tenemos una pirámide cuyos elementos son: b = 2 m; ap = 3 m; su área será: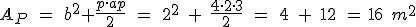 
; donde el perímetro se obtiene multiplicando 4·2.
El volumen de la pirámide anterior, sabiendo que la altura es 4, será: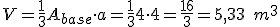 
Caso de estudio
 |
| http://www.cocinaya.com bajo licencia de creative commons |
Ejercicio 6.
En un restaurante nos ponen el siguiente postre.
Tiene una pinta deliciosa, pero queremos saber cuánto chocolate vamos a comernos, por aquello de la dieta.
Con ojos matemáticos, vemos que el chocolate forma una pirámide, así que nos disponemos a tomar medidas para calcular cuánto chocolate nos vamos a comer. Los datos que tomamos son:
lado de la base = 4 cm; apotema = 6 cm; altura de la pirámide = 5 cm.
¿Cuánto chocolate nos vamos a tomar? ¿Qué superficie tendrá el molde con el que se ha hecho la pirámide de chocolate?
 |
| http://planetagadget.com bajo licencia de creative commons |
Ejercicio 7.
En Las Vegas podemos encontrarnos un hotel que tiene forma de pirámide como puedes ver en la imagen. Si buscamos las dimensiones de esta pirámide encontramos que la altura es de 106 m.
Haciendo unos cálculos se tiene que la base de la pirámide tiene un lado de aproximadamente unos 150 m, mientras que la apotema, tiene un valor, también aproximado, de 130 m.
¿Podrías decirme cuánta superficie de cristal se ha utilizado para cubrir la pirámide, y cuánto volumen engloba en su interior?
