3.3. Función cuadrática

Fotografía de tegioz en Flickr. Licencia CC

Desarrollamos a continuación el estudio de otra de las familias con historia en el mundo de las funciones. Nos referimos a las ya mencionadas funciones cuadráticas.

Actividad

Las funciones polinómicas de segundo grado, también llamadas funciones cuadráticas son aquellas cuya ecuación es del tipo:

f(x) = ax² + bx + c, con .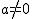

Algunas de sus características principales son:

Su dominio es todo	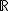El vértice de la parábola es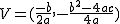
Su gráfica es una parábola, simétrica respecto a eje de simetría que pasa por su vértice.	Cuanto mayor sea el valor absoluto de a, \|a\|, más cerrada será la parábola.
Si a > 0 el vértice de es un mínimo absoluto	Si a < 0 el vértice es un máximo absoluto
Si a > 0 es una función convexa	Si a < 0 es una función cóncava

Entre las funciones cuadráticas podemos distinguir tres tipos especiales, que se corresponden con otras tantas ecuaciones incompletas.

En una función cuadrática f(x) = ax² + bx + c, con .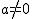

· Si b = 0 y c = 0, la función f(x) = ax² tiene su vértice en el punto (0,0) y su eje de simetría es el eje OY

· Si b = 0 y 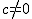, la función f(x) = ax² + c tiene su vértice en el punto (0,c) y su eje de simetría es el eje OY

· Si y c = 0, la función f(x) = ax² + bx tiene su vértice en el punto 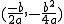y su eje de simetría es la recta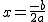

Gráfica

Vértice y puntos de corte con los ejes.

El vértice de cualquier parábola de la forma y=ax² +bx + c es el punto V = (q,p), siendo:

q = -b/2a y p = f(q).O sea, para la primera coordenada aplicamos la fórmula -b/2a y para la segunda, sustituimos en valor obtenido en la función y calculamos la imagen.

Los puntos de corte con el eje de abscisas son (x₁,0) y (x₂ ,0), siendo x₁ y x₂ las soluciones de la ecuación de segundo grado ax² +bx + c = 0.

Al aplicar la fórmula, si recuerdas,dentro de la raíz cuadrada aparecía b² -4ac, por tanto, el número de soluciones y el número de puntos de corte depende del signo de esta operación.


Si *b² - 4ac >0* la parábola corta en dos puntos al eje OX	Si *b² - 4ac =0* la parábola corta en un punto al eje OX	Si *b² - 4ac <0* la parábola no corta al eje OX

Una parábola se puede expresar en función de los puntos de corte con el eje de abscisas de la forma:

y = a·(x - x₁ )·(x - x₂).

El punto de corte con el eje de ordenadas se obtiene haciendo x=0, es decir es el punto (0,c).

(0,c)

Comprueba y practica las características de las funciones cuadráticas con el siguiente applet de Geogebra, realizado por Pablo Espina Brito. Simplemente deberás desplazar los deslizadores para configurar los valores de los coeficientes a, b y c.

Applet alojado en GeoGebra. Licencia CC

Ejemplo o ejercicio resuelto

Fotografía de Autor en Flickr. Licencia CC

Antonio, uno de los empleados de TRANS VELOX en Córdoba, tiene una pequeña discoteca en el centro de la ciudad.

Un día que estuvo en la caseta, invitó al gerente a que se llegara por la noche.

La discoteca abre sus puertas a las nueve de la noche, sin ningún cliente, y las cierra cuando se han marchado todos.

Llamamos x al número de horas que está abierta la discoteca e y al número de clientes que hay en cada momento. Suponemos que la expresión analítica que relaciona al número de clientes con el número de horas que lleva abierta la discoteca es:

y = 60x - 10x².

¿Cuántos clientes tiene a las 10 de la noche? ¿Y a las 12?
¿A qué horas hay en la discoteca 80 personas?
Dibuja la gráfica correspondiente a la expresión anterior.
Determina el número máximo de clientes que van un sábado por la noche a la discoteca y a qué hora ocurre.
Un sábado que estuvo Ignacio había menos de 80 personas y más de 50. ¿A qué hora estuvo?
¿A qué hora cierra Antonio?

Retroalimentación

Si Antonio abre a las nueve de la noche, a las diez ha pasado una hora y el número de clientes será y=60·1-10·1²=50. A las 12 de la noche el número de clientes será y=60·3-10·3²=90.

En la discoteca habrá 80 personas a las 11 de la noche y a la 1 de la madrugada ya que si resolvemos la ecuación de segundo grado que resulta de la igualdad 80 = 60x - 10x², obtenemos x=2 y x=4, es decir, a las 2 y a las 4 horas después de abrir la discoteca.

La gráfica es una parábola con las ramas hacia abajo ya que el coeficiente de x² es negativo. Tiene el vértice en el punto (3,60·3-10·3²)=(3,90), porque x=3 es el punto medio de x=0 y x=6 que son los puntos de corte con el eje OX, ya que son las soluciones de la ecuación de segundo grado 60x-10x²=0.

Gráfica

El número máximo de clientes es 90 y esto ocurre 3 horas después de abrir, es decir, a las 12 de la noche.

Si el sábado que estuvo Ignacio había más de 50 personas y menos de 80, tuvo que ir entre las 10 y las 11 de la noche, o bien entre la 1 y las 2 de la madrugada.

La hora de cierre será cuando se hayan ido todos los clientes, es decir, 6 horas después de abrir, a las 3 de la madrugada.

Ejemplo o ejercicio resuelto

Al rojo vivo.

La función T(t) = 24t - 2t², con 0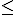t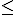12 , devuelve la temperatura, T, en grados centígrados, que alcanza el motor de una máquina de fabricación industrial en función del tiempo, t, en horas, que lleve funcionando.

(a) Realiza la tabla de valores y representa la gráfica de la función.

(b) ¿Qué temperatura alcanza el motor al cabo de 2 horas de funcionamiento?

(d) Observa la gráfica y describe: el dominio, recorrido, la monotonía y la simetría (par/impar) de la función.

Nota: Puedes realizar la representación gráfica con Geogebra o ben en Desmos. A la hora de representarla deberás usar la variable "x" en vez de la variable "t".

Retroalimentación

Como siempre, vayamos por partes.

· Datos

La función T(t) = 24t - 2t² , con 0t12 que devuelve la temperatura que alcanza el motor de la máquina en función del tiempo que lleve funcionando la misma.

· Planteamiento:

Tras leer el enunciado del problema observamos que: la ecuación de la función es de segundo grado y por tanto, su representación gráfica
será una parábola.

A fin de facilitar la representación de la misma al estudiante, se le pide elaborar tabla de valores para posteriormente representarla.

En primer lugar haremos la tabla, posteriormente la representaremos y, finalmente, responderemos a las cuestiones, del resto de apartados, interpretando la gráfica.

· Resolución:

(a)

Tabla de valores:

Tiempo en horas (t)	0	1	2	3	4	5	6	7	8	9	10	11	12
Temperatura en ºC	0	22	40	54	64	70	72	70	64	54	40	22	0

Representación gráfica.

(b) Basta observar la gráfica para comprobar que, a las t=2 horas de funcionamiento la temperatura es T(2)=40 ºC.
También se puede encontrar este valor, buscando en la tabla de valores.

(c) El motor alcanza su temperátura máxima en el vértice de la parábola, esto es, para t=6. A las 6 horas de funcionamiento alcanza su temperatura máxima.

El valor de la temperatura máxima es T(6)=72 ºC, basta observar la gráfica o buscarlo en la tabla de valores.

(d)

- Dominio: [0,12] Tiempo en horas que está en funcionamiento. Sólo funciona 12 h
- Recorrido: (0,72) Temperatura que alcanza el motor en funcionamiento. Rango de temperaturas que alcanza el motor.
- Monotonía: Crece en el intervalo (0,6). Decrece en (6,12). La temperatura va aumentando hasta que alcanza el máximo en el vértice de la parábola, a las 6 horas de funcionamiento. A partir de ahí, decrece hasta alcanzar los 0 grados a las 12 horas.
- Simetría: La gráfica es simétrica respecto de la recta: x=6, que pasa por el vértice de la parábola y es perpendicular al eje OX. No es ni PAR ni IMPAR.

AV - Actividad de Espacios en Blanco

Completa los espacios en blanco indicando qué número de gráfica corresponde a cada expresión analítica.


Gráfica 1	Gráfica 2

Gráfica 3	Gráfica 4

AV - Reflexión

Explica de forma razonada cómo has resuelto la actividad anterior.

Retroalimentación

Las gráficas 1 y 3 corresponden a parábolas abiertas hacia arriba, es decir, el coeficiente de la x² en sus expresiones analíticas es positivo.

La gráfica 1 corta al eje de ordenadas en el punto (0,1), tiene el vértice en el punto (0,1), no corta al eje OX, es simétrica respecto del eje OY, y al desplazarnos una unidad desde el vértice hacia la derecha o hacia la izquierda subimos 2. Resulta de desplazar la parábola y=2x² verticalmente una unidad hacia arriba. Corresponde a la función b) y=2x² +1.

La gráfica 3 corta al eje de ordenadas en el punto (0,-2) y al eje OX en los puntos (-1,0) y (2,0), corresponde a una parábola del tipo y=a(x-x₁)·(x-x₂) donde x₁ y x₂ son los valores de la x en los puntos de corte con el eje de abscisas. Es decir es de la forma y=a(x+1)·(x-2), como pasa por el punto (0,-2) tenemos que -2=a(0+1)·(0-2), por tanto -2=a·(-2), luego a=1. Corresponde a la función

d) y= (x+1)(x-2) = x² -x -2.

Las gráficas 2 y 4 corresponden a parábolas abiertas hacia abajo, es decir el coeficiente de la x² en sus expresiones analíticas es negativo.

La gráfica 2, corta al eje de ordenadas en el punto (0,-2), tiene el vértice en el punto (2,0), corta al eje OX, en el punto (2,0), es simétrica respecto de la recta x= 2, y pasa por el punto (4,-2). Como conocemos tres puntos de la parábola resolvemos el sistema para y=ax²+bx+c:

Sistema . De la primera igualdad obtenemos que c= -2. Sustituimos el valor de c en las otras dos igualdades y tenemos que Sistema , luego a=, b=2 y c= -2.

Corresponde a la función a) y = x²+2x-2 = (x²-4x+4) = (x-2)².

La gráfica 4 corta al eje de ordenadas en el punto (0,-3) y tiene el vértice en el punto (-2,1). Como conocemos el vértice y un punto es una parábola de la forma y=a(x-x_v)²+y_v siendo x_v e y_v las coordenadas del vértice. Es decir, es de la forma y=a(x+2)²+1, como pasa por el punto (0,-3) tenemos que -3=a(0+2)²+1 → -3=4a·+1 → a= -1. Corresponde a la función c) y= -(x+2)²+1 = -x² -4x -3.

Objetivos

En el siguiente vídeo puedes aprender sobre las funciones cuadráticas:

Funciones cuadráticas

Vídeo alojado en Youtube