3.2. Función de proporcionalidad inversa. Función racional
Abandonamos la monotonía de las rectas y de lo lineal y nos adentramos en el mundo de las funciones que representan situaciones de vértigo como cuando nos montamos en "El Iguazú" de Isla Mágica en Sevilla al volver de la feria de Córdoba.
Estas funciones, como recordarás son las hipérbolas.
En el siguiente vídeo te explica qué son las funciones de proporcionalidad inversa:
Actividad
Las funciones de la forma:
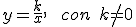
se llaman funciones de proporcionalidad inversa, y su gráfica es una curva que se llama hipérbola.
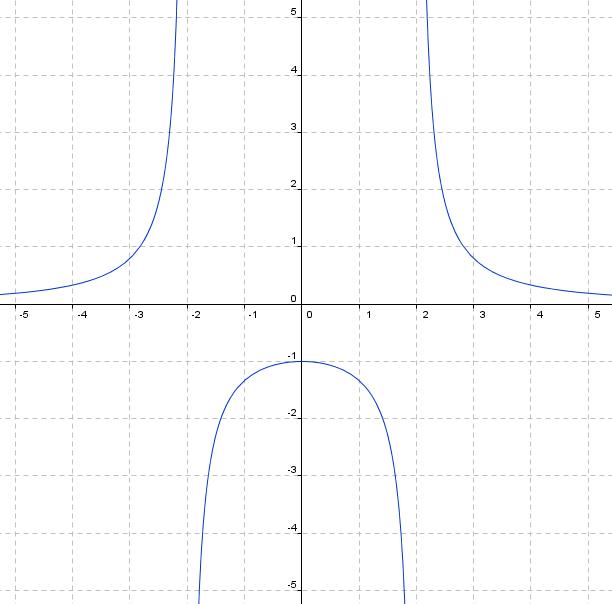
Si k toma valores positivos, la función es decreciente y viene representada en el primer y tercer cuadrante.
Si k toma valores negativos, la función es creciente y viene representada en el segundo y cuarto cuadrante.
En la gráfica de 
, a medida que x va tomando valores cada vez más grandes (se acerca al infinito, a +∞), la y va tomando valores más pequeños (se acerca a cero, es decir, a la recta y=0). Lo mismo ocurre cuando la x toma valores negativos muy grandes (se acerca al infinito, a -∞).
Cuando ocurre esto se dice que la recta y=0 es una asíntota horizontal.
En la gráfica de , a medida que x va tomando valores cada vez más pequeños (se acerca a cero, es decir, a la recta x=0), la y va tomando valores más grandes (se acerca al infinito a +∞ o a -∞).
Cuando ocurre esto se dice que la recta x=0 es una asíntota vertical.
Para x=0, no tiene sentido la función, ya que no podemos dividir por cero.
Una función de la forma es simétrica respecto del origen de coordenadas, es decir, que para valores de la x , la y toma los mismos valores que para valores de (-x) pero cambiados de signo. Si llamamos y=f(x), entonces f es simétrica respecto del origen (simetría impar) si se verifica que f(x)= -f(-x).
AV - Reflexión
 |
En la caseta de TRANS VELOX van a colocar carteles anunciando el plato del día, actuaciones de flamenco, horario, etc.
Nacho les encargó que compraran cartulinas de 24 cm2 y han traído de diferentes tipos: 1x24, 2x12, 3x8 y 4x6.
Cada una de estas cartulinas tiene un área de 24 cm2 aunque distinto perímetro ya que tienen valores diferentes para la base y la altura.
Si llamamos x al valor que toma la base e y al valor de la altura, ¿qué expresión analítica relaciona x con y?
Dibuja una gráfica que represente a todos los rectángulos con un área de 24 cm2.
¿Para qué valores tiene sentido la función?
¿Es creciente o decreciente?
Actividad
Una función racional está formada por un cociente de funciones polinómicas de la forma 
.
La función racional más sencilla es 
que corresponde a una función de proporcionalidad inversa cuya gráfica es una hipérbola.
El dominio de una función racional está formado por el conjunto de los números reales menos aquellos valores de la x que anulan el denominador.
.
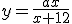para valores de la x desde 1 a 12.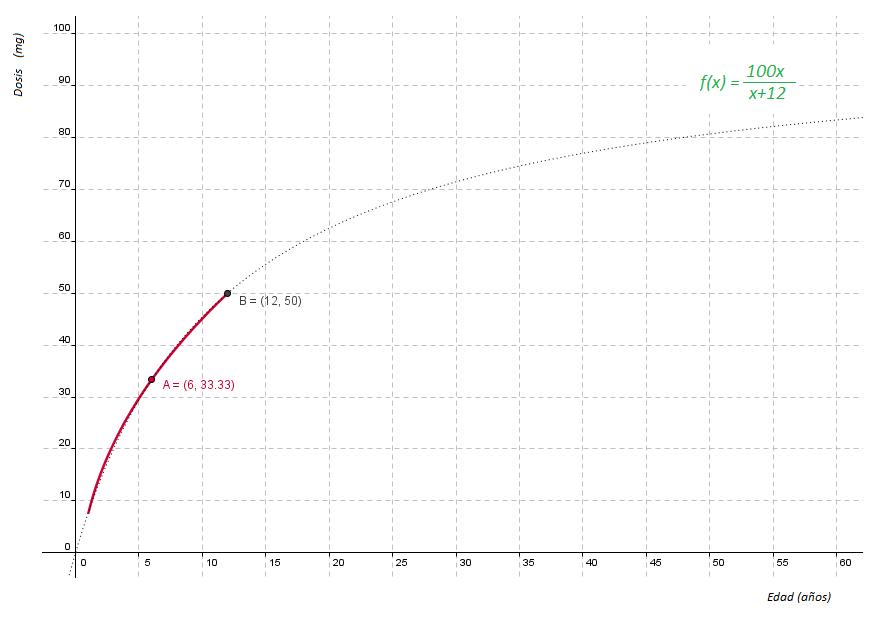
Ejemplo o ejercicio resuelto
 |
Adriana quiere cercar con una cuerda y forma rectangular un rincón de la caseta para guardar las muñecas de Inmaculada.
Si quiere que el área del recinto sea de 2 m2 y el trozo de cuerda no es muy grande, ¿cómo puede expresar el perímetro del cercado en función de una de las medidas del recinto?
¿A qué tipo de función corresponde la expresión encontrada?
¿Para qué valores tiene sentido dicha función?
Construye una tabla de valores para el perímetro y realiza un esbozo de la gráfica de la función.
¿Qué ocurre en la gráfica de la función cuando x toma valores próximos a cero?
¿Qué ocurre cuando la x va tomando valores cada vez más grandes (se acerca al infinito, a +∞)? ¿Y cuando toma valores negativos muy grandes (se acerca al infinito, a -∞)?
AV - Reflexión
Calcula el dominio de las siguientes funciones racionales:
a)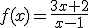 
; b) 
; c)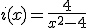 
.
¿Qué función corresponde a la gráfica siguiente? ¿Cuáles son sus asíntotas? Razona la respuesta.
