3.1. Función afín. Función constante
Importante
Las funciones polinómicas de primer grado, también llamadas funciones afines son aquellas cuya ecuación es del tipo f(x) = ax + b
A "a" se le llama pendiente y a "b" ordenada en el origen (punto de corte con e eje Y)
Algunas de sus características principales son:
Su dominio es todo 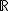 |
Si a > 0, la función es creciente |
| Su gráfica es una recta con pendiente a | Si a < 0, la función es decreciente |
| Pasa por el punto (0,b) [Punto de corte con el eje OY] | |
Dentro de las funciones afines podemos distinguir dos tipos. En una función afín: f(x) = ax + b
· Si a = 0, la función y = b se denomina función constante. Su gráfica es una recta paralela al eje OX, que pasa por el punto (0,b)
· Si a = 0, la función y = ax se denomina función lineal o de proporcionalidad directa ("a" sería la constante de proporcionalidad) y su gráfica es una recta de pendiente a que pasa por el origen de coordenadas (0,0)
Puedes introducir valores en los campos a y b para construir diferentes funciones afines.
Ejemplo o ejercicio resuelto
 |
El precio del trayecto de un taxi tiene un coste fijo de 3 €, más 0,5 € por cada
kilómetro recorrido. Para asistir a la obra de teatro, cogemos uno.
(a) Elabora una tabla de valores de la función
(kilómetros - euros) de nuestro taxi y realiza una representación
gráfica a partir de dicha tabla.
(b) Halla la ecuación de dicha función y calcula su
pendiente.
(c) Si nos cobran 6,25 € por el trayecto hasta el teatro, ¿qué
distancia en metros tiene dicho trayecto?
Nota: Puedes realizar la representación gráfica con Geogebra.
Ejemplo o ejercicio resuelto
Aprovechando que la caseta está a tope, Nacho ha traído unas papeletas para venderlas y sacar dinero para irse de campamento de verano con su grupo scout.
 |
Nacho ha conseguido ganar en un mes 20 euros vendiendo bombones y ahora vende estas papeletas obteniendo un beneficio de 2 € por cada papeleta vendida.
Si x es el número de entradas e y el dinero que tiene Nacho, ¿qué expresión relaciona x con y?
Construye una tabla de valores y representa la gráfica correspondiente.
¿Se trata de una función lineal? ¿Por qué?
¿Cuál es el dominio de definición de la función?
Si Nacho consigue vender 30 papeletas, ¿cuánto dinero tendrá, en total, para el campamento?
AV - Reflexión
A Alejandro, uno de los nietos del gerente de TRANS VELOX le encanta montarse en los coches de choque.
 |
El sábado de feria se organizó un campeonato en la pista más grande del recinto ferial.
La prueba consiste en dar 9 vueltas a la pista en el menor tiempo posible. Cada vuelta tiene 100 metros de longitud.
Alejandro realiza la primera vuelta al circuito a una velocidad constante de 9 km/h, y así sigue hasta dar las 9 vueltas que hacen falta para llegar a la meta.
- ¿Cuánto tardará en dar 4 vueltas?
- ¿Cuánto tiempo tardará en llegar a la meta?
- Cinco minutos después de tomar la salida, ¿cuántas vueltas lleva Alejandro?
- Si llamamos x al número de vueltas e y al tiempo empleado, ¿qué expresión analítica relaciona x con y?
- Dibuja la gráfica correspondiente a la expresión anterior.
AV - Actividad de Espacios en Blanco
 |
Con motivo de la celebración de la semana cultural en una gran ciudad, se ha considerado poner una tarifa plana en el precio de las entradas para acudir a las distintas representaciones teatrales que se celebran esa semana. Se ha establecido una tarifa de 12 euros por persona.
(a) Obtén la ecuación de la función que nos permitirá calcular la recaudación obtenida en cada teatro, en función del número de asistentes.
(b) Si en un determinado teatro se ha completado el aforo para asistir a una obra y se ha recaudado un total de 8400 €. ¿Cuál es el aforo, la capacidad, del teatro? Es decir, ¿cuántas entradas se han vendido?
Actividad
Una función constante es una función afín cuya expresión analítica es de la forma y=k, siendo k un número real, y su gráfica es una recta paralela al eje OX.
 |
Diariamente recibimos llamadas de compañías telefónicas ofreciéndonos ofertas del tipo: "durante este mes pague sólo 10 € por llamadas a móviles y fijos", o bien, "tarifa plana durante 3 meses", etc.
Algo parecido le pasó a Nacho, ya que recibió un mensaje en el móvil diciéndole que por sólo 2 € podía hablar sin coste adicional durante la semana de feria.
Todas estas situaciones se pueden representar mediante un caso particular de función afín, donde no hay ningún tipo de variación. Estamos hablando de funciones constantes.
Ejemplo o ejercicio resuelto
 |
Una de las mañanas que estuvimos en Córdoba, alquilamos un par de bicicletas para dar un paseo por la judería.
Paseando a una velocidad constante fui observando el cuentakilómetros cada minuto y siempre marcaba 20 km/h.
Si x representa el tiempo (minutos) e y la velocidad (km/h), ¿qué expresión relaciona x con y?
Representa en una gráfica los valores obtenidos.
¿Se trata de una función afín? ¿Por qué?
AV - Reflexión
En la siguiente escena de Descartes del I.E.S. Izpisúa Belmonte, vas a practicar calculando la pendiente y la ordenada en el origen de una recta cualquiera de la forma y=mx+k.
Para dar valores a m y k puedes escribir números decimales o fracciones como 5/7 ó -1/2 y pulsar la tecla Intro.
El pulsador azul de la ayuda la activa y el rojo la desactiva. Con la ayuda activada no se cuentan los aciertos.
Objetivos
Función constante. En el siguiente vídeo tienes ejemplos de la función constante: