2. Concepto de función. Características
Las funciones son la aplicación más evidente de las matemáticas en nuestra vida diaria. La idea base del concepto de función, es la de relación de dependencia entre magnitudes o variables. Al estudiar un fenómeno cualquiera, se suele observar que las magnitudes o cantidades que intervienen presentan una relación entre ellas, de forma que una de las magnitudes depende de la otra.
Veamos algunas situaciones cotidianas en las que nos encontramos con dos magnitudes que dependen una de la otra:
 |
 |
| El consumo de combustible de nuestro vehículo depende de la velocidad que llevemos. En este caso llamamos variable independiente a la velocidad y variable dependiente al consumo del vehículo. | El número de escalones de una escalera va a depender de la altura del edificio, por lo tanto, la variable independiente es la altura del edificio y la variable dependiente el número de escalones. |
AV - Actividad de Espacios en Blanco
Importante
Una función real de variable real f es una aplicación que asigna a cada número x de un subconjunto de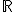 
un único número real y. Escribimos y=f(x) y decimos que y es la imagen de x por f.
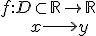
La x recibe el nombre de variable independiente y la y de variable dependiente, ya que el valor de y depende del valor de x.
Para que una gráfica represente una función, a cada valor de x sólo le puede corresponder un valor de y.
Podemos analizar las funciones graficamente, como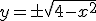 
y cuya gráfica vemos a continuación.
 |
|
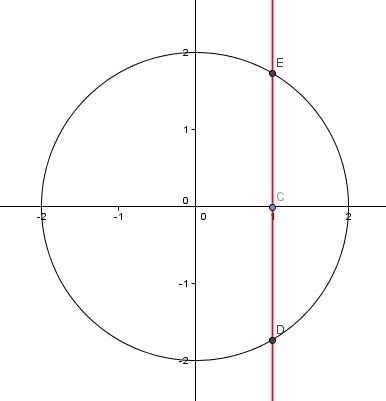Circunferencia
Imagen de elaboración propia
|
Puedes apreciar que para el valor x=1, la función y = f(x) toma dos valores, en este caso 
y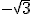 
, por lo que confirmamos que no es función.
AV - Pregunta Verdadero-Falso
Vamos a ver si has comprendido bien el concepto. Para ello marca en las siguientes gráficas las que corresponden con una función y las que no:
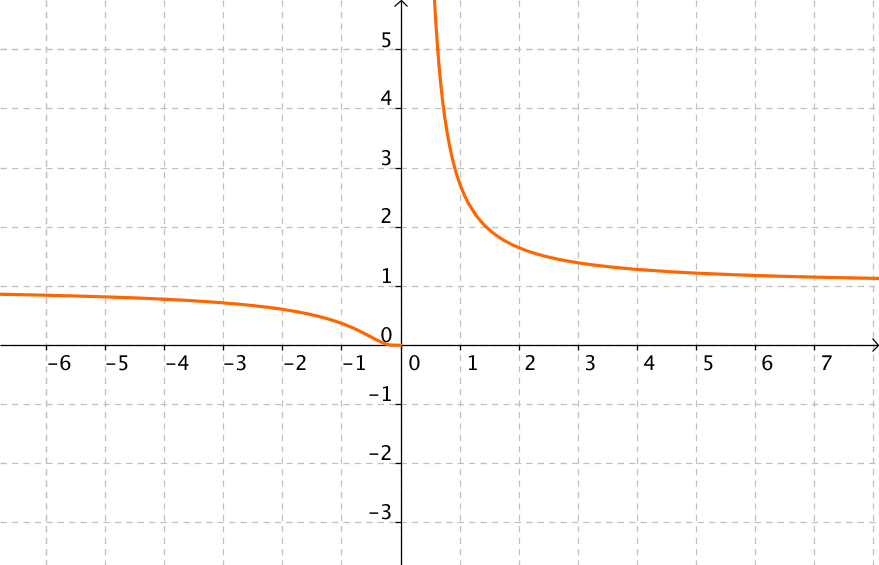
| apartado (a) |
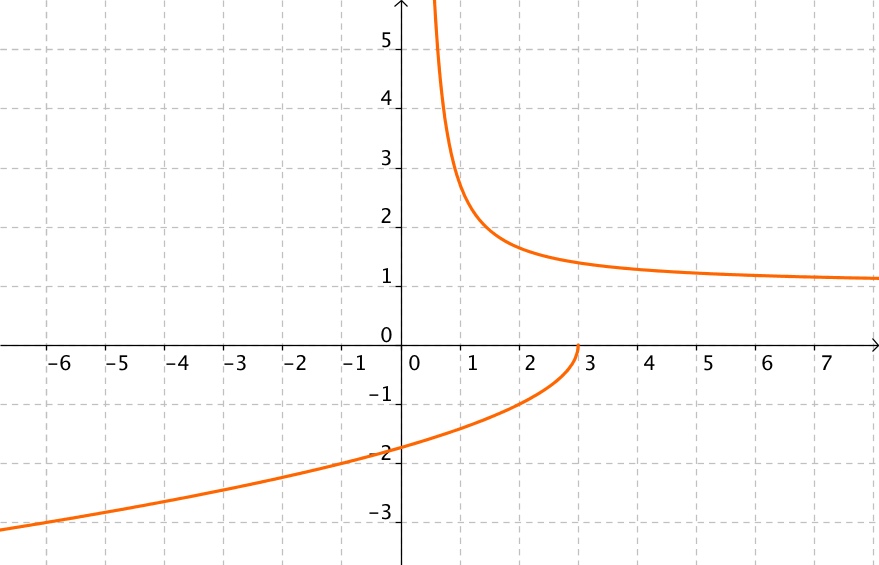
apartado (b) |
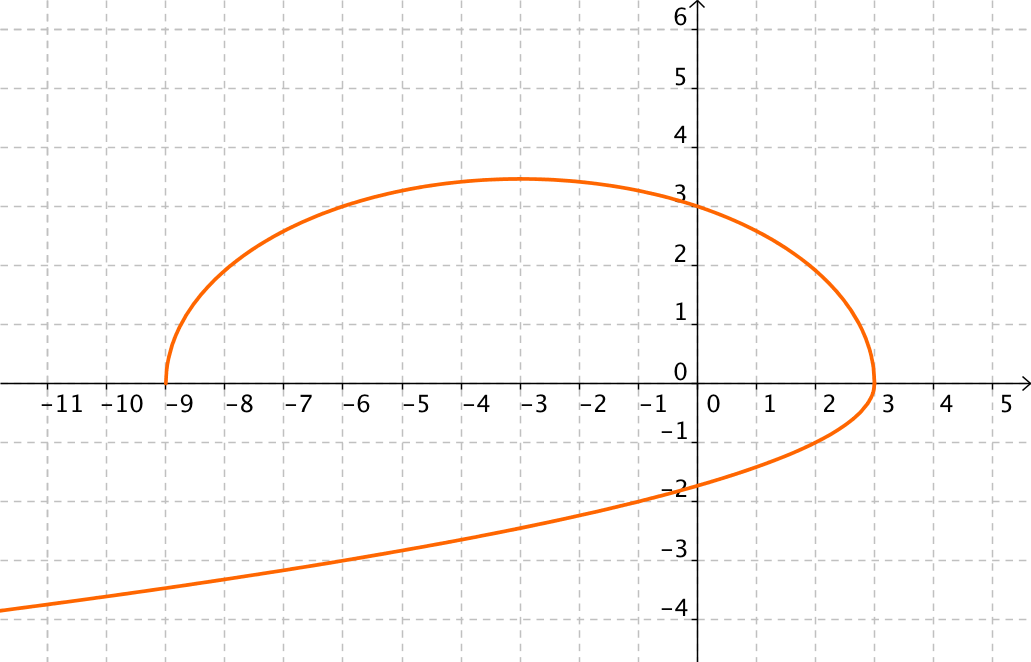
apartado (c) |
 |
 |
 |
Retroalimentación
Verdadero
Para que sea una función, para cada valor de x debe existir, como máximo, un solo valor de y.Retroalimentación
Falso
Para que sea una función, para cada valor de x debe existir, como máximo, un solo valor de y.
En este caso cualquier valor de x ∈ (0,3] tiene más de una imagen.
Retroalimentación
Falso
Para que sea una función, para cada valor de x debe existir, como máximo, un solo valor de y.
En este caso cualquier valor de x ∈ [-9,3] tiene más de una imagen.
A continuación vamos a describir las características que definen a una función. conceptos tales como dominio, recorrido, simetría, etc. serán las propiedades que identifiquen, definan y nos ayuden a entender mejor a cada función en particular.