2.3. Acotación. Corte con los ejes

Fotografía de Jam Adams en Flickr. Licencia CC

¿Te gusta jugar al póker? Imagínate que hubiera una función que te dijera cuánto apostar en cada momento según lo que apuestan tus contrincantes. ¿Genial, no? Imagínate esa vocecita en la conciencia diciéndote hasta aquí, que si no pierdes.

Si representáramos esa función, tendría un tope, un punto del cual no subiríamos más.

Te pongo otra situación, pon un cazo con agua al fuego, pon un termómetro que marque la temperatura del agua, y déjalo ahí, bueno por seguridad quizás es mejor que no lo hagas, pero no cuesta mucho trabajo darse cuenta que la temperatura del agua irá subiendo cada vez más y si no la apartamos del fuego seguirá subiendo. O sea, en este ejemplo, no existiría ese tope o barrera para la función.

En matemáticas, esa barrera se llama cota, y si una función la tiene, decimos que está acotada. Fíjate en las siguientes gráficas:

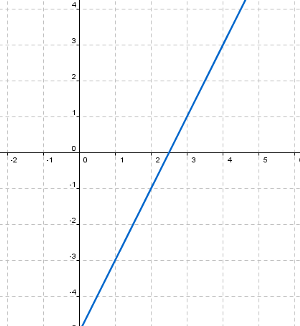
En la primera, la función continúa hacia arriba y hacia abajo, es decir, el recorrido o conjunto imagen es el intervalo (-∞, + ∞). Por tanto, en esta función no existe esa barrera por arriba ni por abajo, luego la función no está acotada.

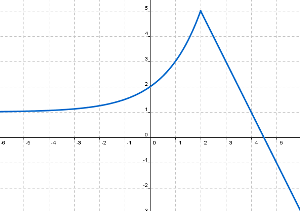
En la segunda gráfica observamos todo lo contrario, ni baja del valor 1, ni se pasa del 5; luego como hemos visto en el punto1.2, Rec(f)=(1,5]. En este caso decimos que la función está acotada, por abajo, la cota inferior es 1 y por arriba, la cota superior 5.

En la tercera gráfica, tenemos una mezcla de los dos casos, por arriba sí está acotada (no se pasa de 5) pero por abajo no (fíjate que la rama de la derecha sigue descendiendo cada vez más.) En este caso, se dice que la función no está acotada, aunque sí lo está superiormente por 5.

Importante

Una función está acotada superiormente si existe un número real K de forma que todos los valores de la función sean menores o iguales que K:

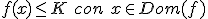
De forma similar, una función está acotada inferiormente si existe un número real K, de forma que todos los valores de la función sean mayores o iguales que K

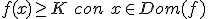
Una función está acotada si lo está superior e inferiormente.

En el siguiente video puedes ver unos ejemplos de funciones acotadas superior e inferiormente.

Función acotada

Vídeo alojado en Youtube

Caso de estudio

Determina las cotas, máximos absolutos y relativos de la función de la función f(x) = x³-3x, cuya representación es

Analizamos la función f(x) = 4-x². Sabemos que está función es de tipo cuadrática, por lo que su vértice se encuentra en 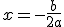siendo la función y = ax²+bx+c, por lo que el vértice lo encoentramos en x= 0, con f(0) = 4. Por lo tanto, cualquier valor por encima de 4 es una cota superior de la función. Veamos graficamente la función y como los valores 5,6 ó 7 son cotas superiores.

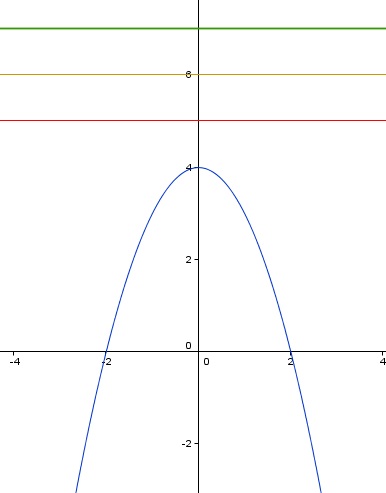
La función f(x) = x⁴ -2x² + 2 tiene la siguiente representación gráfica

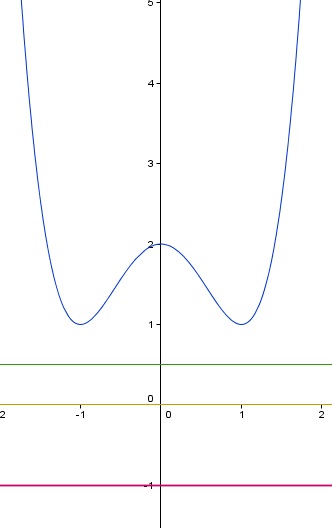
Por lo que podemos afirmar que las valores 0.5, 0 ó -1 son cotas inferiores de la función indicada

Según hemos visto en la definición de cota, nos vamos a encontrar con muchas cotas de una función, por lo que no sería significativo para caracterizar una función hablar de una de sus cotas. Pero si hablamos de una cota superior e inferior particular y que fuera única, si sería un valor interesante para caracterizarla. Para ello vamos a definir el máximo y el mínimo de una función en relación a las cotas de la misma.

Actividad

Decimos que un valor a es el máximo absoluto de una función si pertenece al dominio y es la menor de las cotas superiores.

Analogamente decimos que un valor b es el mínimo absoluto de una función si pertenece al dominio y es la mayor de las cotas inferiores.

Estudiemos de nuevo la función f(x) = x⁴ -2x² + 2, a la cual le calculamos varias cotas inferiores como 0.5 ó -1. Veamos esta nuevo imagen de la función.

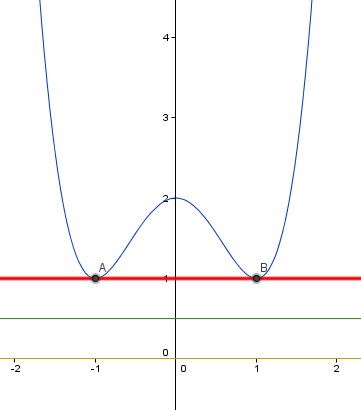
Vemos que el valor -1 es una cota de la función indicada y ademas es el mayor valor de las cotas inferiores, por lo que podemos asegurar que es el mínimo de la función. ¿Para qué valores de x alcanzamos esos valores? En este caso para dos valores. Si observas la gráfica, para los valores x= -1 y x= 1 alcanzamos el valor 1, es decir, f(1) = 1 y f(-1) = 1.

Para los valores x= 1 y x=-1 la función alcanza el mínimo y su valor es 1

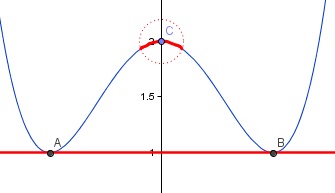
Analicemos, viendo su gráfica, si tiene algún extremo relativo.

Vemos que para el valor de la función tomado para x=0. f(0)=2, es un máximo relativo, ya que en un entorno suyo, es el valor mas alto que toma la función. No globalmente, solo, como decimos, en un entorno de ella.

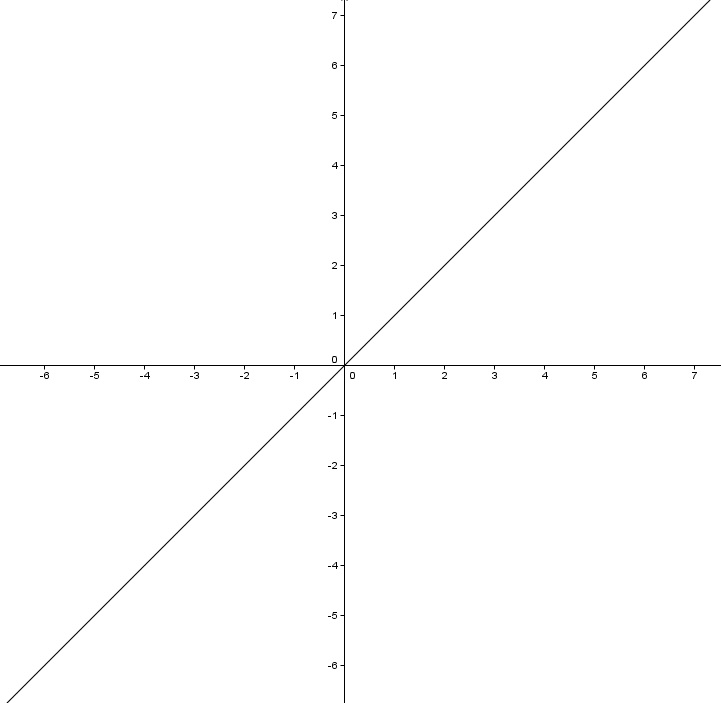
Cabe preguntarnos una nueva cuestión ¿toda función tiene cota superior o inferior? ¿toda función tiene máximo o mínimo?

Analiza graficamente la función y = x y como puedes comprobar no existe ningún valor que sea superior o inferior a los valores de la función, por lo que podemos decir que existen funciones que no están acotadas y al no estarlo, por supuesto, no tienen ni máximo ni mínimo

Importante

Llamamos puntos de corte a aquellos puntos en los cuales la gráfica representada corta al eje de abcisas (eje OX) y/o al de ordenadas (eje OY).

- Los puntos de corte con el eje OX son de la forma (x₀,0). Su coordenada y vale 0.

- Los puntos de corte con el eje OY son de la forma (0,y₀). Su coordenada x vale 0.

Si tenemos la ecuación de la función en la forma y = f(x), hallar los puntos de corte:

· Con el eje OX, equivale a resolver el sistema de ecuaciones: {y=f(x), y=0}

· Con el eje OY, equivale a resolver el sistema de ecuaciones: {y=f(x), x=0}

Curiosidad

La cuenta de resultados.

Fotografía de Eric Caballero en Flickr. Licencia CC

Si llamamos f(x): función de beneficios (ingresos menos costes) de una empresa, donde x representa el tiempo transcurrido en años desde su fundación.

(a) f(0) punto de corte con el eje OY, nos indicará el coste de la empresa. Es decir, al comienzo no existen ingresos luego, nos devolverá, cuánto ha sido la inversión necesaria para poner en marcha la empresa.

(b) Si para algún año, x, tenemos que f(x)=0, punto de corte con el eje OX, nos indicará que en el año x, la empresa ha obtenido un beneficio igual a 0 €. Ha ingresado lo mismo que ha gastado.

(c) Si f(x) > 0 indicará que la empresa ha obtenido beneficios. Por el contrario, si f(x) < 0 indicará que la empresa ha obtenido pérdidas durante ese año.

Ejemplo o ejercicio resuelto

SEPTIEMBRE 2011. ANDALUCÍA

Halle el dominio, los puntos de corte con los ejes, y las asíntotas de la función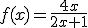

Ejercicio valorado en 1'25 puntos.

Retroalimentación

Como verás, estamos ante una función racional. El dominio de la función se calcula viendo en qué puntos se anula el denominador, ya que como sabes tienen de dominio todos los números reales salvo dichos puntos. Por tanto resolvemos:

Y por tanto el dominio es:

Calculemos los puntos de corte:

Una función corta al eje OX o eje de abscisas cuando f(x)=0, en puntos de la forma (x, 0). Por tanto:

Y deducimos que corta al eje OX en el punto (0, 0)

Una función corta al eje OY o eje de ordenadas cuando damos a x el valor cero (punto de la forma (0, y)). Por tanto:

Y deducimos que corta al eje OY en el punto (0, 0). En este caso coincide con el único punto de corte del eje OX.

En cuanto al cálculo de las asíntotas, aprenderás a calcularlas en el próximo tema. En este primer tema has aprendido a deducirlas a partir de la gráfica. Veamos la gráfica de esta función, que aparece en color azul, y las asíntotas en color rojo:

Las ecuaciones de las asíntotas son:

Asíntota horizontal: y = 2
Asíntota vertical: x = -1/2 (fíjate que coincide con el punto x en el que no hay dominio de la función, lo cual ocurre en las funciones racionales en la gran mayoría de las ocasiones)

AV - Actividad de Espacios en Blanco

Observa con detenimiento las gráficas de las funciones representadas y rellena a continuación los huecos en cada una de los apartados:


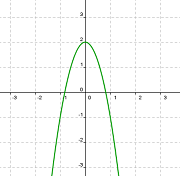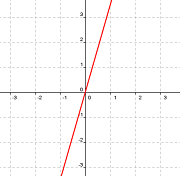Gráfica 1	Gráfica 2

Llamaremos f(x) a la función representada en la Gráfica 1 y g(x) a la representada en la Gráfica 2.

· f(-1) = Rellenar huecos (1):JXUwMDc1JXUwMDFj , f( Rellenar huecos (2):JXUwMDY4 ) = 2 , f(1) = Rellenar huecos (3):JXUwMDc1JXUwMDFj

· f es una función Rellenar huecos (4): en el intervalo (-,0] porque -1 Rellenar huecos (5):JXUwMDY0 0 y f(-1) ≤ f (0)

· f es una función Rellenar huecos (6): en el intervalo [ Rellenar huecos (7):JXUwMDY4 ,+) porque Rellenar huecos (8):JXUwMDY4 < Rellenar huecos (9):JXUwMDY5 y f(0) ≥ f (1)

· f corta al eje OY en el punto de coordenadas ( Rellenar huecos (10):JXUwMDY4 , Rellenar huecos (11):JXUwMDZh )

· f corta al eje OX en Rellenar huecos (12):JXUwMDZh punto/s

· g es una función estrictamente Rellenar huecos (13):

· g(0) = Rellenar huecos (14):JXUwMDY4

· g corta el eje OX en el punto ( Rellenar huecos (15):JXUwMDY4 , Rellenar huecos (16):JXUwMDY4 ) y al eje OY en el punto ( Rellenar huecos (17):JXUwMDY4 , Rellenar huecos (18):JXUwMDY4 )

Habilitar JavaScript