5. Matriz inversa
En el ejemplo que hicimos en el apartado anterior, multiplicábamos una matriz de precios por una matriz de pedidos y obteníamos la matriz de costos. ¿Te imaginas que al cabo del año quisiéramos buscar algún precio pero el catálogo se ha perdido entre los múltiples papeles de la oficina? ¿Podríamos saber algún precio si dispusiéramos de las facturas totales y de la cantidad pedida?
El problema que se plantea es encontrar la matriz A sabiendo B y C en el producto A·B = C, o sea, encontrar una de las dos matrices que se están multiplicando.
Si las matrices fueran números, está claro que el problema se reduciría a hacer una división. Por ejemplo, en 2·x = 6, está claro que x vale 3, pues 6:2 = 3.
¿Es posible hacer lo mismo con matrices? O, lo que es igual, ¿existe la división de matrices?
La respuesta es no, no se pueden dividir matrices, aunque sí existe una operación que viene a ser equivalente y que conlleva el cálculo de la matriz inversa.
Veamos cómo se realiza el cálculo de la matriz inversa. ¿Recuerdas del curso pasado el método de Gauss para resolver un sistema de ecuaciones lineales con tres incógnitas? Básicamente, había que, mediante una serie de transformaciones en las que multiplicábamos las filas por números y las sumábamos después, "hacer" ceros por debajo de la diagonal principal.
Algo similar vamos a hacer aquí.
Existen diversos métodos para calcular la matriz inversa, pero el que nosotros vamos a usar es el de Gauss-Jordan.
En la siguiente presentación te mostramos paso a paso cómo se hace. Vamos a calcular sólo inversas de matrices 2x2 para no complicar mucho el asunto.
La siguiente escena de geogebra te muestra los pasos que debes dar para hallar la inversa de una matriz por el método de Gauss-Jordan. Para ello, lo único que tienes que hacer es introducir los elementos de la matriz 2x2 cuya inversa quieras hallar en los casilleros correspondientes que figuran en la matriz de arriba. En el caso de que no se pueda hallar la matriz inversa, la aplicación te lo indicará.
Importante
La inversa de una matriz A, que representaremos por A-1, es otra matriz de la misma dimensión y que cumple la siguiente condición:
A·A-1 = I y A-1·A = I
Puesto que las dos matrices tienen la misma dimensión, para que el producto se pueda hacer, la matriz A tiene que ser cuadrada. Es decir, la inversa de una matriz sólo tiene sentido para matrices cuadradas.
Como ya hemos visto más arriba, uno de los métodos de los que disponemos para hallar la inversa de una matriz A es el método de Gauss-Jordan.
Resumiendo, se trata de situar en una misma matriz los elementos de la matriz A, en la parte izquierda, y los elementos de la matriz identidad en la parte derecha. Mediante las transformaciones elementales que conocemos por el método de Gauss:
- Intercambiar filas o columnas entre sí,
- multiplicar o dividir una fila o columna por un número distinto de cero y
- multiplicar dos filas o columnas por dos números y sumar o restar el resultado y colocarlo en el lugar de cualquiera de las dos filas o columnas mencionadas,
tenemos que conseguir que en la parte izquierda de la matriz aparezca la matriz identidad.
Una vez conseguido, el resto de la matriz que nos quede en el margen derecho será la matriz inversa.
AV - Reflexión
Te proponemos tres matrices para que practiques:
1) 
2) 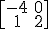
3) 
Para saber más
Si la matriz es de dimensión mayor, el procedimiento es igual, sólo que más largo.
En esta página puedes ver cómo se hace y, si quieres, puedes ver, además, este vídeo en el que se explica cómo se calcula la inversa de una matriz cuadrada 3x3. Y si quieres practicar, aquí tienes.
Ecuaciones con matrices.
En muchas situaciones es necesario plantear ecuaciones con matrices donde la incógnita será una matriz (sin ir más lejos, en el ejemplo con el que hemos introducido el apartado). El procedimiento es similar al de una ecuación de primer grado, despejar la incógnita. Ahora bien, dado que una matriz no puede pasar dividiendo al otro miembro de la ecuación, se debe multiplicar por la matriz inversa.
En este enlace te explican cómo se hace esto y, además, tienes algunos ejercicios por si quieres practicarlo.