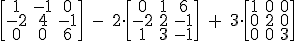4.2. Producto por un escalar
Imagino que te ha resultado fácil lo de sumar y restar matrices y que los ejercicios que te propusimos te han salido a la perfección. Bueno, pues vamos a dar otro pasito para empezar a multiplicar matrices. Lo que ocurre es que con las matrices eso del producto ya no es tan evidente y ni tan siquiera es necesario que las dos matrices sean de la misma dimensión. Es más, ¡a veces el producto de dos matrices de la misma dimensión no se puede calcular! Y es que, en el producto, ya no sirve eso de multiplicar los elementos que están en la misma posición, sino que habrá que seguir otro procedimiento.
No te preocupes que con los ejemplos que te vamos a proponer lo vas a entender y, sobre todo, vas a entender el por qué de ese procedimiento.
Para empezar, tenemos que tener en cuenta el tipo de multiplicación que vamos a hacer, si vamos a multiplicar por un número, un vector (matriz columna), o una matriz por una matriz.
Importante
El producto de una matriz A por un número real k es otra matriz de la misma dimensión que A, cuyos elementos se obtienen multiplicando cada elemento de A por k.
A=(aij) → k·A = (k·aij)
En este vídeo te combinamos ya las dos operaciones que llevamos, esto es, sumar o restar y multiplicar por un número. Recuerda que una multiplicación siempre se hace antes que una suma o una resta.
Vídeo de lasmatematicas.es alojado enYoutube
Para saber más
El elemento neutro de esta operación es el 1, pues si multiplicamos nuestra matriz A por 1, nos quedamos igual, esto es, con la matriz A.
1·A = A
Las otras propiedades que cumple son la distributiva respecto de la suma de matrices, la distributiva respecto de la suma de escalares y la asociativa mixta. Si quieres verlo con más detalle, sigue este enlace.
AV - Reflexión
Vamos a practicar un poco antes de seguir. Haz los siguientes cálculos con matrices:
a) 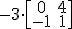
b) 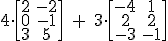
c)