3.1. Definición
Una matriz de m filas y n columnas es un conjunto de números reales ordenados en filas y columnas. La posición de cada elemento aij queda determinado por sus dos subíndices: el primero indica la fila y el segundo la columna.
Las matrices suelen representarse como:
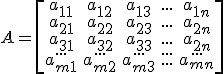
que es una matriz con m filas y n columnas. Se dice que es una matriz de orden mxn.
Cuando la matriz tiene el mismo número de filas que de columnas se dice que es una matriz cuadrada.
Reflexión
La siguiente tabla nos indica las distancias en kilómetros entre las distintas sucursales que la empresa TRANS Velox, mencionada en el apartado anterior, tiene en la provincia de Sevilla:
| Cazalla de la Sierra |
Écija | Morón de la Fra. |
Pilas | Sevilla | |
|
Cazalla |
- | 105 | 131 | 118 | 80 |
| Écija | 105 | - | 74 | 128 | 89 |
| Morón de la Fra. |
131 | 74 | - | 110 | 66 |
| Pilas | 118 | 128 | 110 | - | 39 |
| Sevilla | 80 | 89 | 66 | 39 | - |
Escribe la matriz A, asociada a la tabla de distancias e indica los valores de los siguientes elementos de la matriz: a13, a22, a35, a41, a54.
Antes que nada, vamos a recordar qué es una matriz, pues aunque ya lo hemos ido viendo en lo que llevamos de tema, no está de más volverlo a recordar para que nos quede bien clara la idea.
Como ya se ha mencionado, una matriz es un conjunto de números reales ordenados en filas y en columnas. Cada número o elemento de ese conjunto queda referenciado por la posición que ocupa, escribiéndose con subíndices el número de fila y de columna que ocupa.
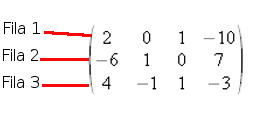
Cada elemento es como si fuera un balcón de un edificio y, para llamarlo, debemos indicar la fila y la columna que ocupa, empezando la numeración de arriba abajo en las filas y de izquierda a derecha en las columnas:
 |
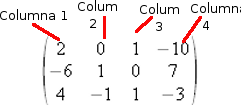 |
Así, por ejemplo, el elemento a21 es -6, pues es el valor del número que está en la fila 2 y en la columna 1, o el elemento a31 es 4.
Está claro, ¿no?
Ejemplo o ejercicio resuelto
Ya hemos visto cómo la información recogida en tablas se podía expresar mediante matrices. Vamos a ver que la información verbal también se puede adecuar a una matriz. ¿Recuerdas a la empersa TRANS VELOX? Pues, durante la primera quincena del mes, han seguido el número de portes que han hecho en una de las rutas y los han clasificado en cuatro grupos, según el peso de los artículos transportados.
En la primera semana, transportaron 20 sobres o documentos, 48 paquetes de menos de 2 kg, 25 de entre 2 y 5 kg y 31 paquetes de más de 5 kilos. En la segunda semana, los portes han sido de 14 sobres, 50 paquetes de menos de 1 kg, 20 portes de entre 2 y 5 kg y 38 paquetes de más de 5 kg.
¿Podemos expresar esto como una matriz?
AV - Reflexión
Antes de seguir, vamos a practicar un poco con lo que llevamos hasta ahora. Fíjate en la siguiente situación:
La empresa Infomax monta ordenadores de mesa y portátiles. Para cada clase de ordenador la empresa dispone de tres tipos según la calidad y cantidad de sus componentes: alta, media y baja.
En el mes de julio, montaron en ordenadores de mesa 20 de calidad alta, 40 de calidad media y 40 de calidad baja, mientras que, en el caso de los portátiles, montaron 32 de calidad alta, 28 de calidad media y 43 de calidad baja.
Por otro lado, en cada ordenador de mesa, se necesitan 4 horas de trabajo en el montaje y 6 en la instalación del software necesario, mientras que, para portátiles portátiles son necesarias 7 y 8 horas respectivamente. Pues bien, has de averiguar las matrices A y B que determinan el número de ordenadores según el tipo y la calidad así como el número de horas de montaje e instalación con el tipo de ordenador, respectivamente. Además, indica la dimensión de ambas matrices.
Importante
Una medida importante que hace referencia a las matrices es la que llamada dimensión de la matriz.
La dimensión de una matriz indica el tamaño de la misma, es decir, el número de filas y columnas, y se expresa como m x n, siendo m el número de filas y n el de columnas.
En general, si la matriz es de la forma:
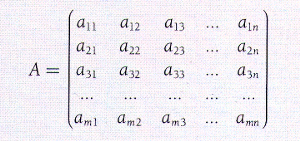
la dimensión es m x n.
Por ejemplo, en la matriz la dimensión es 3 x 4.
la dimensión es 3 x 4.