2.4 Plano inclinado

La mayor parte de los movimientos no tienen lugar en un plano horizontal, sino que presentan un cierto desnivel. Una buena aproximación para estos casos consiste en suponer que nuestro móvil se desplaza sobre un plano inclinado.

¿Tenemos fuerzas diferentes a las ya estudiadas? Pues no. Están presentes la fuerza peso (ejercida por el planeta Tierra), la fueza Normal (ejercida por el plano), la fuerza de rozamiento y en algunos casos una fuerza aplicada. Sin embargo la presencia de un plano inclinado nos fuerza a cambiar el sistema de referencia y tomar los ejes en la dirección paralela y perpendicular a dicho plano. Como consecuencia tendremos que calcular las componentes cartesianas de la fuerza peso que ya no estará alineada con ningún eje.

Reflexiona

Manipula el siguiente simulador variando el ángulo del plano inclinado y responde a las siguientes preguntas:

  1. A medida que aumentamos el ángulo de inclinación del plano, ¿cómo varía la componente del peso paralela al plano?
  2. A medida que aumentamos el ángulo de inclinación del plano, ¿cómo varía la componente del peso perpendicular al plano?

Simulación de Jesús Peñas en Educaplus 

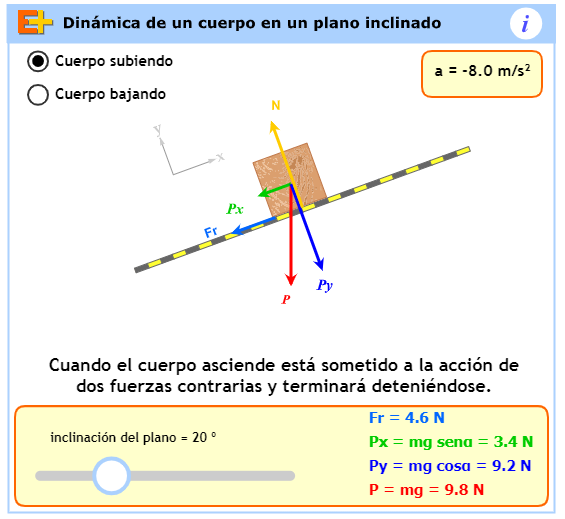
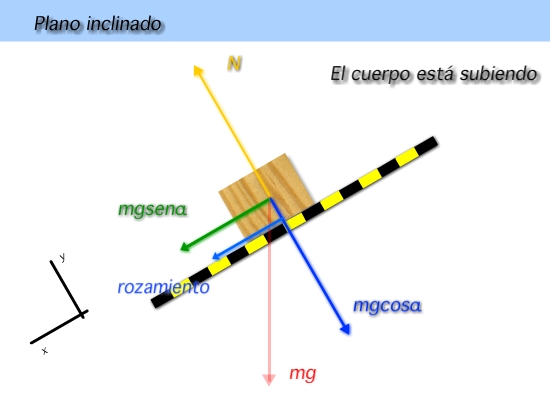
Estudiaremos primero el caso de un cuerpo que asciende por un plano inclinado con rozamiento.

Imagen de elaboración propia

Aplicamos la segunda ley de Newton a cada eje teniendo en cuenta qué fuerzas actúan a favor y en contra:

- m\cdot{}g\cdot sen{\alpha } - F_R = m\cdot a_x \\ N - m\cdot{}g\cdot\cos{\alpha }=0

Sustituyendo la fuerza de rozamiento por su valor como producto del coeficiente de rozamiento por la normal, se obtiene:

- m\cdot{}g\cdot sen{\alpha } - \mu\cdot N = m\cdot a_x \\ N = m\cdot{}g\cdot\cos{\alpha }

Calculando el valor de la normal con la segunda ecuación y sustituyendo en la primera ecuación podemos despajar la aceleración del cuerpo que evidentemente será negativa. Esto quiere decir que al cabo de un tiempo la velocidad se hará cero y el cuerpo se parará.

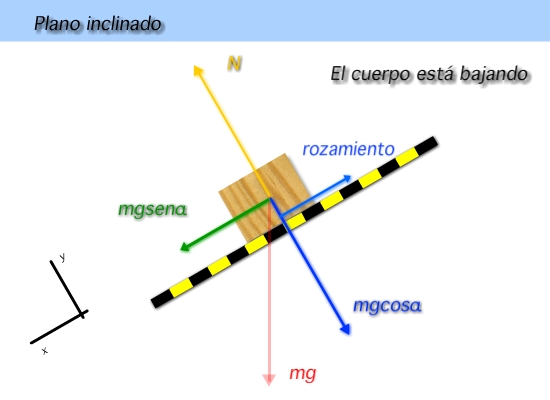
Veamos ahora qué ocurre cuando el cuerpo desciende por un plano inclinado con rozamiento.

Imagen de elaboración propia

Aplicamos la segunda ley de Newton a cada eje teniendo en cuenta qué fuerzas actúan a favor y en contra:

m\cdot{}g\cdot sen{\alpha } - F_R = m\cdot a_x \\ N = m\cdot{}g\cdot\cos{\alpha }

Sustituyendo la fuerza de rozamiento por su valor como producto del coeficiente de rozamiento por la normal, se obtiene un sistema de dos ecuaciones con dos incógnitas:

m\cdot{}g\cdot sen{\alpha } - \mu\cdot N = m\cdot a_x \\ N = m\cdot{}g\cdot\cos{\alpha }

Calculando el valor de la normal con la segunda ecuación y sustituyendo en la primera ecuación podemos despajar la aceleración del cuerpo. Dependiendo del ángulo de inclinación y del coeficiente de rozamiento tendremos una aceleración positiva o negativa.

Caso práctico

Vamos a analizar el caso de un cuerpo que asciende o desciende por un plano inclinado con rozamiento. Supongamos primero que el cuerpo está subiendo.

Simulación de Jesús Peñas en Educaplus

1. Fija un ángulo de 20º. En la dirección perpendicular al plano, ¿hay aceleración? ¿Qué puedes concluir gracias a este dato?
2. Al hacer crecer el ángulo de inclinación del plano inclinado, ¿cómo varía el valor de la Normal?
3. Al aumentar el ángulo de inclinación, ¿cómo varía la fuerza de rozamiento?
4. ¿Por qué la aceleración en la dirección paralela al plano es negativa cuando el cuerpo asciende?
5. Supón ahora que el cuerpo está descendiendo, ¿hacia adónde apunta ahora la fuerza de rozamiento?
6. Modifica el ángulo de inclinación. ¿Qué ocurre con el signo de la aceleración?

Comprueba lo aprendido

 Simulación de Jesús Peñas en Educaplus

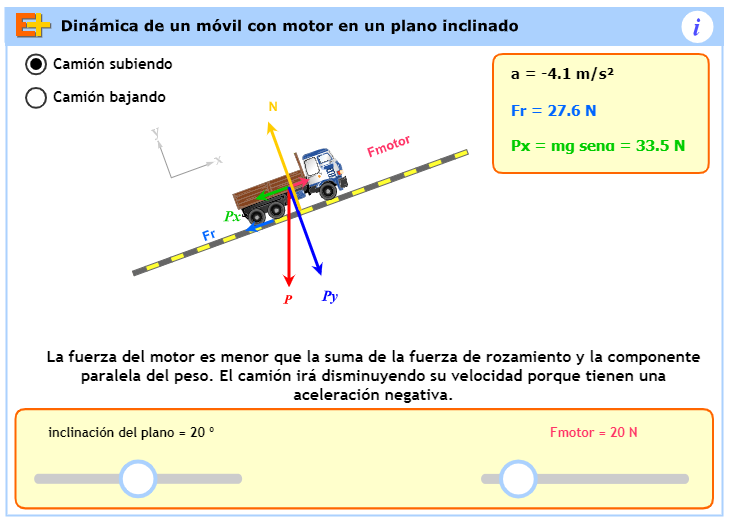
 Un camión se encuentra en una cuesta. El motor del camión ejerce una fuerza hacia arriba cuando este asciende.

Para una inclinación de 15º, si la fuerza del motor es , las fuerzas en contra del movimiento son que las fuerzas a favor por lo que la aceleración es negativa . El camión irá hasta pararse.

Para la misma inclinación, si la fuerza del motor es , las fuerzas del movimiento son mayores que las fuerzas por lo que la aceleración es positiva . El camión irá subiendo cada vez con .

 

Habilitar JavaScript

Para saber más

Habitualmente, en deportes como el ciclismo no se habla del ángulo de inclinación de una carretera o pista, sino que se indica en forma de porcentaje. Así, es normal escuchar cómo la parte más dura de un puerto tiene un desnivel del 12%, u observar una señal que indica pendiente prolongada del 5% durante los próximos 2 kilómetros. ¿Qué significan estos porcentajes?
Los topógrafos utilizan una fórmula que relaciona la distancia horizontal recorrida con la vertical:
% Pendiente = Distancia en vertical · 100/Distancia en horizontal
Sin embargo, no es sencillo calcular la distancia en horizontal que hemos recorrido, por lo que, dado que los ángulos en carretera no suelen ser muy grandes, puede tomarse el espacio recorrido sobre ella en lugar de la distancia en horizontal, ya que el error en estos casos es mínimo. Así, la fórmula habitual para calcular el ángulo a partir del desnivel es:
sen α = (metros ascendidos / metros recorridos) → α = arcsen (metros ascendidos / metros recorridos)
Imagen de Staycoolandbegood en Wikipedia. CC0

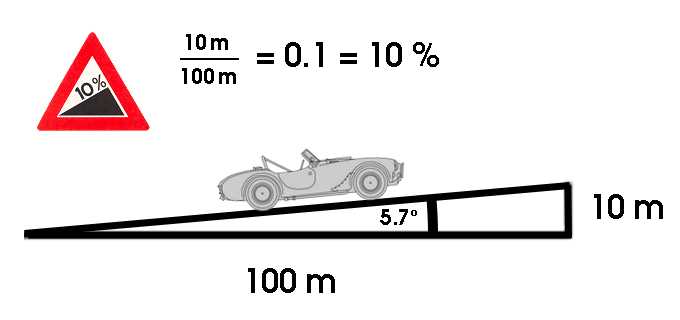
Caso práctico

Una motorista se encuentra ascendiendo un puerto con una pendiente constante del 5%. Si la masa total del conjunto motorista-moto es de 300 kg, responde a las siguientes cuestiones:
a) ¿Cuál es el ángulo de inclinación de la carretera respecto a la horizontal?
b) Dibuja el esquema de fuerzas que actúan sobre el sistema.
c) Calcula el valor mínimo del coeficiente de rozamiento entre las ruedas y el asfalto para que la moto, con el motor apagado y completamente frenada, no comience a deslizarse hacia abajo.

d) Determina la fuerza que deberá realizar el motor para subir con velocidad constante, supuesto un coeficiente de rozamiento µdi = 0.5