3.2. Monotonía y extremos
Monotonía (Crecimiento y decrecimiento)
Seguro que en los últimos meses (si no años) has oído cientos de veces expresiones como "es necesario promover el crecimiento" o "estamos abocados hacia un decrecimiento...".
 |
| Imagen de elaboración propia |
Sí, son ideas asociadas a la economía y extrapolables a otros muchos ámbitos de nuestra vida diaria y como no, a las funciones que, por cierto, ya deberían formar parte de esa cotidianidad.
Ambos conceptos están relacionados con la monotonía. Cuando a algo le damos la cualidad de monótono, queremos decir que no cambia, que no varía, que siempre tiene un mismo tono. Ya sabes, asociamos algo monótono a algo aburrido, precisamente por eso, porque mantiene unas mismas características, sin variación alguna.
Pues bien, en Matemáticas, cuando hablamos de estudiar la monotonía de una función, lo que buscamos es analizar los intervalos en los que no se produce cambio alguno entre crecimiento y decrecimiento.
Estudio de las características de f a través del análisis de su derivada
El crecimiento y el decrecimiento de una función son conceptos que ya hemos estudiado antes ¿lo recuerdas? Básicamente una función es creciente si, al aumentar la variable independiente, 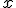 , también aumenta el valor de la función,
, también aumenta el valor de la función, 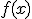 . Es decreciente, si al aumentar el valor de
. Es decreciente, si al aumentar el valor de 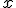 , disminuye el de
, disminuye el de 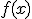 . No olvides que las gráficas se "leen" de izquierda a derecha.
. No olvides que las gráficas se "leen" de izquierda a derecha.
 |
| Imagen de elaboración propia |
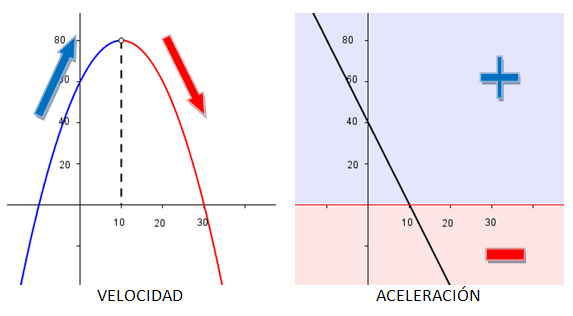 |
| Imagen de elaboración propia |
Mira ahora la gráfica de la aceleración ¿qué ocurría hasta el minuto 10? Que la aceleración era positiva (pues su gráfica queda por encima del eje de abscisas), y si la aceleración es positiva quiere decir que el coche acelera y por tanto su velocidad aumenta.
A partir del minuto 10, la aceleración es negativa (su gráfica queda por debajo del eje de abscisas), por tanto está decelerando y la velocidad disminuye.
Seguro que en física has estudiado que la aceleración es la derivada de la velocidad. Acabamos de ver una relación entre el signo de la aceleración, y el crecimiento y el decrecimiento de la velocidad. Esta misma relación se da entre cualquier función derivable, y su derivada.
Importante
Cuando hablamos de monotonía, nos estamos refiriendo al comportamiento de una función respecto a su crecimiento o decrecimiento.
Sea 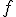 una función derivable en un intervalo
una función derivable en un intervalo 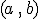 , entonces es:
, entonces es:
- Creciente en el intervalo
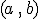 si
si 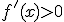 en todo el intervalo
en todo el intervalo 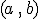
- Decreciente en el intervalo
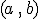 si
si 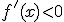 en todo el intervalo
en todo el intervalo 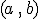
Si pinchas en la siguiente imagen, descubrías una escena de geogebra con dos ejemplos, una función polinómica y una racional, en la que puedes comprobar que se cumple lo que acabamos de ver:
| Función f(x) |
Derivada f ' (x) |
| Creciente | Positiva (con línea discontinua) |
| Decreciente |
Negativa (con línea discontinua) |
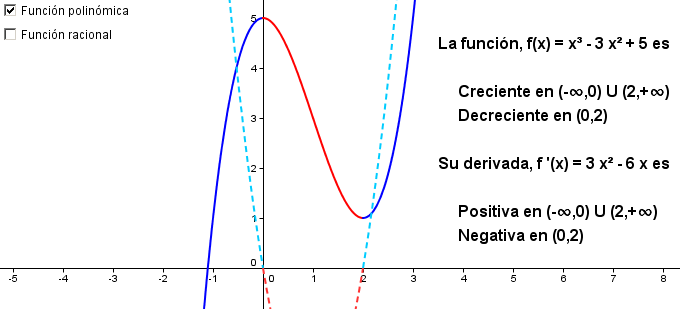 |
| Captura de pantalla de una escena de GeoGebra de Saúl Valverde |
Como ya hemos comentado, lo relevante del importante anterior, es que ya no es necesario dibujar la gráfica para estudiar la monotonía. A continuación tienes un ejercicio resuelto para que veas cómo hacerlo. Después hay uno que tendrás que resolver tú.
|
Presentación en Slideshare por saulvalper. |
AV - Actividad de Espacios en Blanco
En una empresa están teniendo pérdidas económicas, por lo que deciden poner en marcha una serie de medidas a lo largo de los próximos 6 meses con las que pretenden remontar y obtener beneficios al finalizar dicho periodo.
Según sus cuentas, los beneficios obtenidos por la empresa al poner en marcha el plan vienen dados por la función 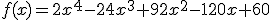 donde
donde 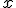 es el número de meses.
es el número de meses.
Vamos a comprobar si con este plan de medidas la empresa mejorará los beneficios. Para ello tendrás que estudiar los intervalos de crecimiento y decrecimiento de los beneficios de la empresa.
Extremos (máximos y mínimos)
Estamos acostumbrados a oir hablar de temperaturas máximas y mínimas todos los días en las noticias. De hecho, es una frase muy habitual la de "se ha alcanzado una máxima de 40º de temperatura". En la siguiente gráfica, de la AEMET, en la que podemos ver la temperatura que ha hecho en Málaga desde las 19h del 13 de abril a las 18h del día siguiente. Puedes comprobar que:
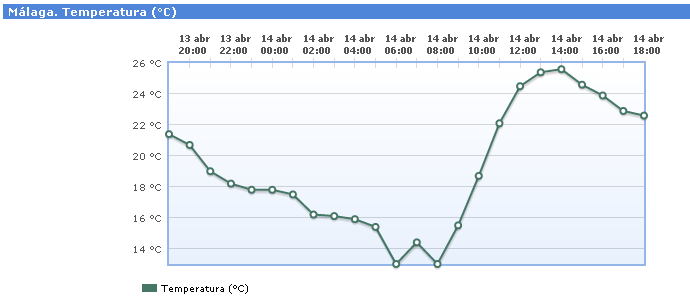 |
| Captura de pantalla del AEMET del 14/04/12 en Málaga |
- La temperatura máxima se alcanza a las 14h del 14 de abril (25,6ºC).
- La temperatura mínima se alcanza a las 6h y a las 8h del 14 de abril (13ºC).
- A las 7h del 14 de abril hay un máximo relativo, pues es la temperatura más alta en un pequeño periodo de tiempo (de las 6 a las 8h).
Para poder averiguar la temperatura máxima o mínima necesitamos una tabla de datos observados o una gráfica como la anterior, pues la temperatura local no la podemos expresar con una función derivable.
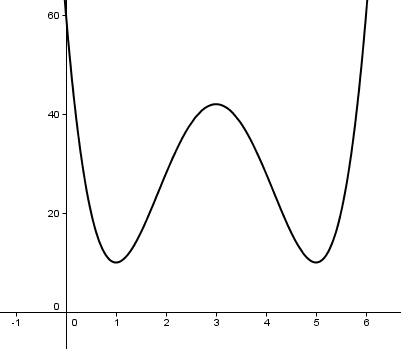
Veamos por tanto qué ocurre en la siguiente función, y comparemos con su derivada:
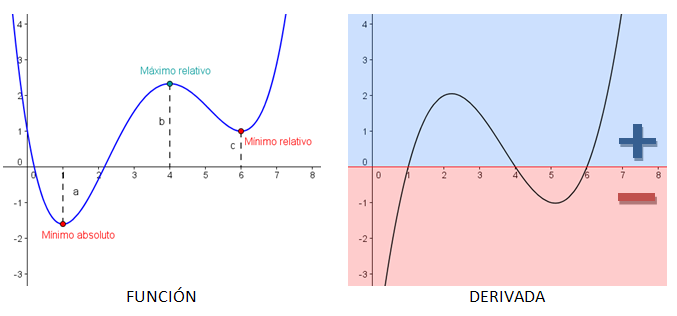 |
| Imagen de elaboración propia |
A la izquierda tenemos una función 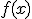 y a la derecha su derivada
y a la derecha su derivada 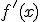 .
.
- Mínimo: si te fijas en los dos mínimos, a su izquierda la función es decreciente y a la derecha es creciente ¿qué quiere decir eso para la derivada? Como vimos en el apartado anterior, equivale a que a la izquierda la derivada es negativa y a la derecha positiva (como puedes ver en la gráfica de la derivada). Pues si en ese punto la derivada pasa de negativa a positiva, quiere decir que debe ser nula.
- Máximo: en el máximo pasa algo parecido, pero en este caso pasamos de función creciente a decreciente, es decir, de derivada positiva a negativa. Al igual que antes, en ese punto la derivada debe ser nula.
Importante
Una función 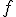 , continua y derivable en un intervalo
, continua y derivable en un intervalo 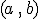 , alcanza sus máximos y mínimos relativos en los puntos del intervalo
, alcanza sus máximos y mínimos relativos en los puntos del intervalo 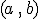 en los que
en los que 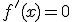 . Además, si estudiamos la segunda derivada:
. Además, si estudiamos la segunda derivada:
- Máximo relativo:
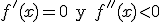 .
. - Mínimo relativo:
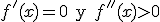 .
.
Para que veas cómo podemos hallar máximos y mínimos con la derivada, mira los siguientes ejemplos:
| Vídeo en YouTube por juanmemol |
| Presentación en Slideshare por saulvalper |
AV - Pregunta de Selección Múltiple
Solution
Solution
Solution
Solution
Caso de estudio
 |
Curso 2009/2010
Dada la función  determine las regiones de crecimiento y decrecimiento de la función.
determine las regiones de crecimiento y decrecimiento de la función.