1.1. Variación media y variación instantánea

|
| Fotografía en Flickr por Guillermo Puglia bajo CC |
Tasa de variación media
Imagínate que este viaje por las funciones lo hacemos en tren. En este medio de locomoción no tenemos la oportunidad de mirar el velocímetro como en un coche para saber a qué velocidad nos desplazamos. Pero si la curiosidad nos inunda podemos acudir a un simple cálculo, hacer el cociente entre el espacio recorrido y el tiempo que hemos tardado en recorrerlo, de esta forma, obtendremos la velocidad media entre dos instantes del viaje.
Esta velocidad media, nos permite comparar la variable dependiente (el espacio) y la variable independiente (el tiempo), es decir, nos podemos hacer una idea de si el vehículo circula rápido o lento en un determinado periodo de tiempo.
Reflexión
Importante
Dada una función 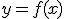 se llama variación media de
se llama variación media de 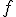 en un intervalo
en un intervalo 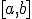 al cociente:
al cociente:
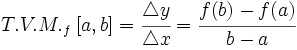 |
Al ser la variación media un cociente de variaciones las unidades en que se expresa son también cociente de unidades. Por ejemplo la velocidad media se mide en km/h, la temperatura media en ºC/h, el precio medio en €/kg…
En el siguiente vídeo de juanmemol puedes ver un ejemplo resuelto del cálculo de la tasa de variación media de la función 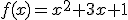 en el intervalo [-2,1]:
en el intervalo [-2,1]:
Observa la siguiente escena de Geogebra. En ella puedes ver el cálculo de la tasa de variación media de dos puntos cualesquiera (solo tienes que manipular los puntos verdes) y la relación que guarda con la recta secante a la curva 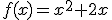 en esos dos puntos.
en esos dos puntos.
Importante
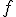 en el intervalo
en el intervalo 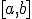 es la pendiente de la recta secante a la gráfica de
es la pendiente de la recta secante a la gráfica de 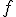 que pasa por los puntos
que pasa por los puntos 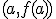 y
y 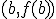 .
.
 y
y 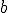 coinciden).
coinciden).

|
| Fotografía en Flickr por brewbooks bajo CC |
Tasa de variación instantánea o variación media centrada en un punto
¿Qué hace un radar en la carretera para calcular la velocidad de un vehículo? Toma dos fotografías en intervalo de tiempo reducido y a partir de ellas calcula la velocidad media que ha de ser bastante aproximada a la velocidad que llevaba el vehículo en cualquier instante intermedio. Algo similar se hace en matemáticas para calcular la tasa de variación de una función en un determinado instante. Se centra la consideración en dicho instante y se introducen pequeñas variaciones a partir del mismo.
Si ahora volvemos a las funciones y, teniendo en cuenta que 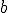 es mayor que
es mayor que  , se puede expresar
, se puede expresar 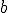 como
como 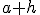 , donde
, donde 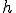 sería un número real y positivo, y de esta forma la tasa de variación media se podría expresar con la siguiente fórmula:
sería un número real y positivo, y de esta forma la tasa de variación media se podría expresar con la siguiente fórmula:
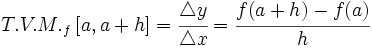
Si 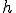 se aproxima a cero, el punto
se aproxima a cero, el punto 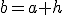 se aproximará al punto
se aproximará al punto  y la tasa de variación media tenderá entonces a un valor que denominamos tasa de variación instantánea de la función
y la tasa de variación media tenderá entonces a un valor que denominamos tasa de variación instantánea de la función 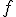 en el punto
en el punto  . Que si hablamos en términos de velocidad, sería justo la que marca el velocímetro de nuestro coche en un determinado momento.
. Que si hablamos en términos de velocidad, sería justo la que marca el velocímetro de nuestro coche en un determinado momento.
Importante
La tasa de variación instantánea de una función 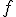 en el punto
en el punto  es:
es:
Caso de estudio
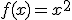 en
en