3. Movimiento ondulatorio
Vamos a estudiar ahora las ondas a partir del caso más simple: las ondas armónicas (recuerda, aquellas en que cada punto que recibe la perturbación adquiere un MAS).
Actividad
Cualquier onda se puede expresar como combinación de ondas armónicas. (Fourier, 1822).
En la siguiente animación te mostramos un movimiento ondulatorio sencillo. Se trata de una onda que viaja a lo largo de una cuerda. Todos los puntos de la cuerda se mueven. Cada punto se aleja del eje x una distancia (elongación) y que va cambiando en el tiempo.
| Animación de Fernando Martínez en Geogebra. CC |
Concentra tu atención en el punto rojo. Si te fijas, comprobarás que describe un movimiento oscilatorio respecto de la posición y=0 m. Este movimiento se repite y se denomina ciclo u oscilación. El tiempo que tarda en repetirse es el período.
Las ondas armónicas tienen un carácter periódico, concretamente, presentan doble periodicidad; y, por ello, para caracterizarla se puede utilizar una serie de magnitudes que permanecen constantes durante su propagación, algunas ya han sido tratadas al estudiar el movimiento armónico simple.
Las magnitudes que se expondrán a continuación se pueden agrupar en tres bloques: las dependientes del foco emisor, las dependientes del medio y, por último, las dependientes del medio y del foco. En resumen:
| Magnitudes características de las ondas | ||
| Dependientes del foco emisor | Dependientes del medio | Dependientes del medio y del foco |
| Período (T) | Velocidad de propagación (v) | Longitud de onda (λ) |
Frecuencia (f o  ) |
||
| Frecuencia angular (ω) | Número de ondas (k) | |
| Amplitud (A) | ||
Veámoslas:
- Elongación (
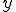): es la separación de un punto con respecto a su posición de equilibrio en un instante determinado. Su unidad en el S.I. es el metro. - Amplitud (A): es la máxima elongación que sufren las partículas del medio sometidas al movimiento ondulatorio. Su unidad en el S.I. es el metro.
- Período (T): es el tiempo que tarda en volver a reproducirse una onda. Su unidad es el S.I. es el segundo. Recuerda que la frecuencia (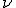) es la inversa del período, y se mide en Hz.
- Frecuencia angular o pulsación (ω = 2π/T = 2π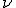): es el número de periodos comprendidos en 2π unidades de tiempo y el valor depende de la rapidez o celeridad con que oscila o vibra el objeto. Se mide en rad/s en el S.I. Se usa el valor de 2π debido a que el valor coinciden con el número de radianes que tiene una circunferencia.
Período, frecuencia y pulsación son propiedades características del oscilador armónico que hace de foco emisor de ondas y es independiente de la amplitud del movimiento. Esto quiere decir que sus valores permanecen constantes cuando la perturbación se propaga por un medio o cambia de un medio de propagación a otro.
Importante
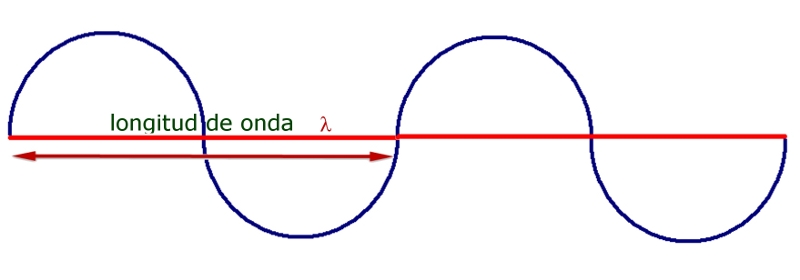
- Longitud de onda (
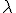): es la distancia que separa dos puntos consecutivos en fase. La longitud de onda es también la distancia de una onda completa. Su unidad en el S.I. es el metro. Desde otro punto de vista, corresponderá a la distancia que se ha propagado una perturbación en un período de tiempo (T), por consiguiente, no depende de los puntos que son tomados por referencia para determinarla, teniendo cierto carácter absoluto.
|
|
- Velocidad de fase o de propagación (v) de la onda: es la rapidez con se transmite la perturbación por un medio. Esta magnitud depende del medio y está relacionada con la longitud de onda y el período de la onda. Su unidad en el S.I. es m/s
- Número de ondas (k): es la cantidad de ondas completas contenidas en una distancia 2π metros. Esto se puede expresar como:
Actividad
Amplitud, periodo, frecuencia y pulsación no varían al pasar de un medio a otro.