3.1 Ecuación de propagación de una onda
Ya sabemos que las ondas tienen unas características un tanto singulares.
Su doble periodicidad, una con respecto al tiempo (periodo) y otra referida a la distancia con respecto al centro emisor (longitud de onda), las hace especiales. Luego, para poder edificar un modelo adecuado desde una perspectiva matemática, se debe encontrar una expresión adecuada que contemple esta doble periodicidad.
![]()
A la expresión anterior se le denominará ecuación de ondas y con la misma se pretende conocer el valor de la magnitud cuya propagación constituye la onda en cualquier punto del espacio que sea afectado o alterado por la misma y en cualquier instante después de que el foco emisor diera comienzo a la perturbación. Expuesto de otra forma, asignando a la variable ![]() el valor de la perturbación, la ecuación nos servirá para valorar la modificación del medio a una distancia
el valor de la perturbación, la ecuación nos servirá para valorar la modificación del medio a una distancia ![]() concreta y en un tiempo
concreta y en un tiempo ![]() determinado desde el inicio de la emisión.
determinado desde el inicio de la emisión.
Volvamos sobre la onda que se propaga por una cuerda. Cada punto de esta onda se mueve con un MAS. Concretamente la ecuación del punto de la cuerda que está en x=0 m es:
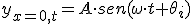
y la ecuación queda aún más sencilla.
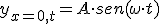
Por lo tanto, un punto que diste x metros del origen, tendrá una ecuación de movimiento tal que así:

que resulta de introducir el retraso en llegar la pertubación. Ese lapso de tiempo se puede calcular dividiendo la distancia x que separa este punto del origen por la velocidad con que se propaga la onda. Si hacemos una serie de operaciones, la ecuación adquiere un aspecto más homogéneo y fácil de recordar:
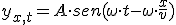
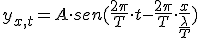

Esta es la ecuación de una onda que viaja por una cuerda y que tiene una amplitud A, un período T y una longitud de onda  .
.
Esa misma ecuación se puede expresar de otra forma empleando los conocimientos de la trigonometría:
En la siguiente simulación puedes modificar tanto la longitud de onda, como la amplitud, el período y el sentido de propagación de la onda y observar cómo cambia su ecuación. Pulsa sobre el botón de la esquina inferior izquierda para ver cómo se propaga cada onda después de establecer sus características.
| Animación de Antonio González García en Geogebra. CC |
Ejemplo o ejercicio resuelto
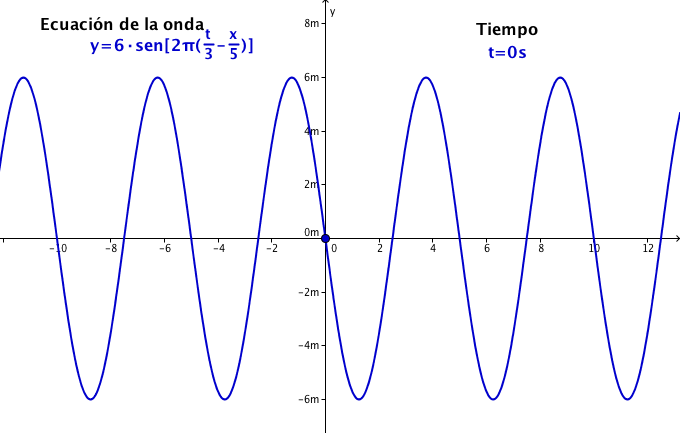
La ecuación de una onda es:

Usando la ecuación, determina las siguientes magnitudes o características de la onda:
2. Su período.