2.2 Dinámica del MAS
 |
| Imagen de Marc Lagrange en Wikipedia. CC |
Para abordar este apartado vamos a recordar algo que ya vimos en la unidad 1 (tema de Dinámica):
los cuerpos elásticos (muelles) se deforman cuando se les aplica una fuerza, pero recuperan su forma original al dejar de actuar la fuerza. La deformación producida y la fuerza aplicada están relacionadas de forma que el alargamiento del muelle es directamente proporcional a la fuerza aplicada:
![]()
siendo F la fuerza aplicada, ΔL el alargamiento del muelle y k la constante elástica o recuperadora del muelle.
Esta es la ley de Hooke.
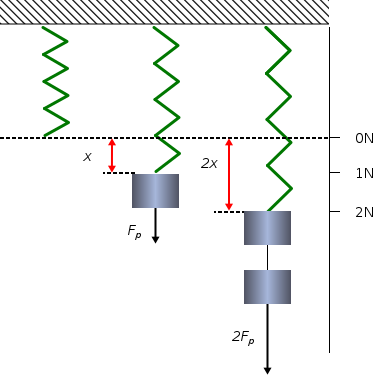
Sabemos que, una vez estirado, el muelle tiende a su estado inicial, gracias a una fuerza recuperadora, proporcional a la deformación del resorte, aunque de sentido opuesto, y que cumple la ley de Hooke:
Esta fuerza recuperadora pretende llevar de nuevo al sistema al equilibrio.
La fuerza restauradora (recuperadora o elástica) es variable, y tendrá sentido contrario al movimiento (siempre se dirige hacia la posición de equilibrio). Puedes verlo en la animación siguiente:
| Animación de Fco Javier Robles Martín, Elvira Martinez y Carlos Romero en Geogebra. CC |
Ya ves que el valor de F varía: cuanto mayor es el alargamiento o la compresión del muelle, mayor será la fuerza.
Aplicando la segunda ley de Newton:
Bajo la acción de una fuerza elástica, un cuerpo seguirá un movimiento armónico simple.
Nueva definición del MAS
Es posible, por todo lo anterior, redefinir el MAS:
El movimiento armónico simple de un punto material se da cuando, si por una perturbación se pierde el equilibrio estable, este se hallará sometido a una fuerza restauradora que intente devolver el sistema al equilibrio. Esta, proporcional al desplazamiento de su posición de equilibrio, es opuesta al movimiento de forma que realice un movimiento de vaivén en torno a una posición de equilibrio.
La fuerza restauradora ha de cumplir la ecuación siendo x la separación de la posición de equilibrio (elongación) y K la constante recuperadora del muelle.
Caso práctico
Si se cuelga un cuerpo de 2 kg en dos muelles, vemos que estos se alargan 2,3 cm y 30 cm. Determina el valor de la constante elástica de cada muelle.
Conocemos las ecuaciones de movimiento del MAS, si recordamos la de la aceleración: ![]()
Combinando con la expresión de la fuerza restauradora y la segunda ley de Newton:
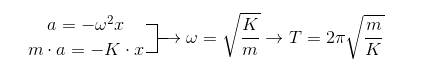
Estas expresiones importantes muestran cómo la frecuencia angular ω y el período T del movimiento armónico simple dependen de las características del oscilador (de k).