2.1 Cinemática del MAS
¿Cuáles son las ecuaciones del movimiento armónico simple?
Las ecuaciones de un MCU ya las conocemos: 
Recuerda, las coordenadas 
e 
se pueden escribir en función de R (el radio de giro) y 
(el ángulo):
 |
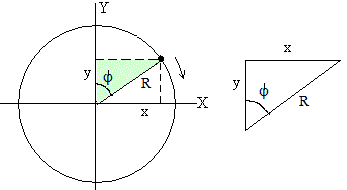Como la posición cambia con el tiempo, se debe colocar el ángulo en función del tiempo.
Si el movimiento no comienza para un ángulo cero, se ha de añadir un elemento: el desfase 
.
Quedan por tanto las ecuaciones el MCU:
Hemos comprobado, con la animación del apartado anterior, que la coordenada de ambos movimientos coincidía. Esto quiere decir que ya sabemos la ecuación de la posición de un MAS.
Posición en un MAS
Se describe la posición de un objeto que se mueve en el eje X siguiendo un movimiento armónico simple con la siguiente ecuación:
El valor de la coordenada es la separación del punto de equilibrio respecto del que oscila nuestro móvil y la denominamos elongación. El valor máximo de la elongación se obtiene cuando el seno toma valor 1 o -1:
Como amplitud (A) es el valor máximo de la elongación, la ecuación anterior quedará:
 |
Actividad
Se puede escribir la ecuación en función del seno o del coseno indistintamente, y esto es gracias a que son expresiones equivalentes, solo se diferencian en la fase inicial (las dos formas simplemente presentan un desfase de 
)
Así las expresiones 
y 
son equivalentes.
Objetivos
Fase (): el argumento de la función sen . Es el valor angular que nos permite calcular la posición del móvil en cualquier instante.
Fase inicial (): valor de la fase en el instante en el que comienza la medida.
Objetivos
Como sabrás, la función seno es periódica y se repite cada 
,
 |
| Imagen de Keytotime en Wikipedia. CC0 |
por tanto, el movimiento se repite cuando el argumento de la función seno 
se incrementa en , es decir, cuando transcurre un tiempo T se cumple:
Es por ello que: 
Caso práctico
La posición de un objeto que se guía por una fuerza recuperadora viene definida perfectamente por una expresión matemática que puede ser expresada con una función seno o coseno. Si un oscilador armónico tiene una pulsación ω y amplitud A:
Expresa, tanto en función del seno como en función del coseno, la ecuación del movimiento de ese oscilador que cambia de posición en el eje "x" en las siguientes situaciones con respecto a la posición inicial propuesta:
a) En la posición de equilibrio y con sentido hacia los valores positivos de la elongación.
b) En la posición de equilibrio y con sentido hacia los valores negativos de la elongación.
c) En el valor positivo máximo de la elongación.
d) En el punto más alejado de la posición de equilibrio en los valores negativos.
e) En el punto medio de la amplitud, situado en los valores negativos y moviéndose hacia los valores positivos.
Velocidad del MAS
Del MAS sabemos que se trata de un movimiento rectilíneo pero no uniforme porque la velocidad varía. Piensa en el cuerpo que cuelga de un muelle, se frena cada vez que se acerca a los puntos de máxima separación del punto de equilibrio hasta pararse (pasa de una velocidad máxima en el punto de equilibrio a una velocidad cero en los extremos).
La ecuación de velocidad de un cuerpo con M.A.S. se obtiene derivando la ecuación de posición respecto del tiempo
La fórmula de la velocidad en función de la elongación será: 
Puedes comprobar que para x = 0 → v = Aω
Por tanto la velocidad máxima se produce en el centro (x = 0) y en los extremos (donde x = A) se cumple que v = 0.
Aceleración del MAS
Derivando la expresión de la velocidad respecto del tiempo obtendremos la aceleración del cuerpo:
Se deduce fácilmente la relación entre la aceleración y la elongación en un MAS:
El valor máximo se alcanza en los extremos de la oscilación, al contrario que la velocidad. Y en el punto medio de equilibrio a = 0, ya que x = 0.
Actividad
| ecuación | relación con x | condición de anulación | condición de máximo | valor máximo | |
| velocidad |  |
|
|
cuando x = 0 (en el punto de equilibrio) |
|
| aceleración |  |
|
 cuando x = 0 (en el punto de equilibrio) |
cuando x es máxima (en los extremos) |  |
