2. Sistemas de tres ecuaciones con tres incógnitas

Hay multitud de situaciones y problemas cuya solución se obtiene resolviendo sistemas con muchas ecuaciones e incógnitas. Si ya tiene mérito resolver problemas usando dos ecuaciones, imagínate con tres, cuatro,... resulta casi un ejercicio de "malabarismo". Gauss dio una respuesta a este problema resolviendo sistemas con el mismo número de ecuaciones que incógnitas.

malabares

Imagen de ihor_konst en Pixabay. Licencia Pixabay

El método de resolución de Gauss lleva su nombre debido a que él lo describió en un artículo en el que detallaba todos los cálculos que hizo para determinar la órbita del asteroide Pallas. Los parámetros de la órbita tenían que determinarse mediante observaciones del asteroide durante seis años (1803-1809), lo que dio lugar a un sistema de seis ecuaciones con seis incógnitas.

Gauss demostró cómo resolver estas ecuaciones reemplazándolas sistemáticamente por un nuevo sistema en el que sólo la primera ecuación tenía seis incógnitas, la segunda tenía cinco, la tercera tenía sólo cuatro, y así sucesivamente, hasta que la última ecuación tenía una sola incógnita. Este método también se denomina método de reducción en cascada o de triangulación.

Importante

El método de Gauss consiste en obtener sistemas equivalentes al que queremos resolver, cada vez más sencillos, hasta obtener uno muy simple con forma triangular. El sistema que buscamos debe tener una única incógnita en su última ecuación, dos en la penúltima,..., y todas las incógnitas en la primera ecuación.

Las soluciones se obtienen desde la última ecuación a la primera, es decir, resolviendo, en primer lugar, la última, sustituyendo el valor obtenido en la penúltima y resolviendo la ecuación resultante, y así sucesivamente.

En el siguiente vídeo se explica de manera sencilla, clara, y mediante un ejemplo, el método de Gauss. En este caso, se va a resolver un sistema de tres ecuaciones con tres incógnitas.

Vídeo de lasmatematicas.es alojado en Youtube

Comprueba lo aprendido

Ejercicio Resuelto

Resolver el siguiente sistema por el método de Gauss:

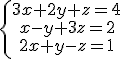Retroalimentación

Paso 1

Dado que el coeficiente de la incógnita x en la segunda ecuación es 1, podemos cambiar el orden de las ecuaciones primera y segunda. Al hacer esto, obtenemos un sistema equivalente al anterior:

Paso 2

Para obtener el sistema escalonado que buscamos hemos de sustituir la segunda ecuación por otra con dos incógnitas (y y z). Para ello, hemos de aplicar la transformación consistente en multiplicar la primera ecuación por un número y sumar el resultado a la segunda, de tal forma que en la ecuación resultante solo queden coeficientes para las incógnitas y y z (y que sean distintos de 0).

En nuestro caso, bastará con multiplicar la primera ecuación por -3 (que coincide con el coeficiente que acompaña a la incógnita x en la segunda ecuación con el signo contrario) y sumarla con la segunda como puede apreciarse a continuación:

De esta forma, el sistema resultante, equivalente al primero, es el siguiente:

Paso 3

A continuación, vamos a aplicar el mismo procedimiento a la primera y tercera ecuaciones, de manera que sustituyamos la tercera por otra con dos incógnitas (y y z). Para ello, hemos de aplicar la transformación consistente en multiplicar la primera ecuación por un número y sumar el resultado a la tercera, de tal forma que en la ecuación resultante solo queden coeficientes para las incógnitas y y z (y que sean distintos de 0).

En nuestro caso, bastará con multiplicar la primera ecuación por -2 (que coincide con el coeficiente que acompaña a la incógnita x en la segunda ecuación con el signo contrario) y sumarla con la tercera como puede apreciarse a continuación:

El sistema resultante, equivalente al primero, es el siguiente.

Paso 4

Finalmente, volvemos a aplicar el procedimiento a la segunda y tercera ecuaciones, de manera que sustituyamos la tercera por otra con una sola incógnita (z). Para ello, hemos de aplicar la transformación consistente en multiplicar la segunda y tercera ecuaciones por dos números (que, en nuestro caso, coincidirán con los coeficientes de la otra) de manera que, al sumarlas, obtengamos una ecuación que tenga únicamente coeficiente para la incógnita z.

obteniendo, finalmente, el sistema de ecuaciones escalonado deseado:

La solución es sencilla de hallar si comenzamos a resolver desde la tercera ecuación y vamos "escalando" hasta la primera. De esta forma, la solución del sistema es:

2. Sistemas de tres ecuaciones con tres incógnitas

Importante

Comprueba lo aprendido