2.3. Aproximación
 |
| Imagen de albert2278 en Pixabay. Licencia CC |
Aproximación
Si lo piensas bien, existen muchas situaciones en nuestra vida cotidiana donde utilizamos los números de manera aproximada.
Lo hacemos normalmente por dos motivos:
- Porque es conveniente o no es necesario dar una cantidad exacta que sí conocemos.
- O porque no tenemos forma de medir esa cantidad con exactitud.
Cuando vamos a comprar frutas o verduras y pedimos un kilo o tres cuartos de algún producto, si nos fijamos bien en la cantidad que marca la balanza, casi nunca el frutero coloca la cantidad exacta de la mercancía que hemos solicitado. "Pasa un poco del kilo", nos dice el comerciante; o "le faltan 35 gramos para los tres cuartos".
Importante
Si en un número decimal, a partir de un determinado orden, sustituimos todas las cifras de orden inferior por ceros, obtendremos otro número decimal que se dice una aproximación del primero (hasta el orden fijado).
La siguiente imagen está tomada de una infografía de Visual20, en los que se comparan los edificios más altos del mundo con el proyectado por el arquitecto español Santiago Calatrava y que pasará a ser la más alta del mundo una vez terminada.
Te planteamos la siguiente reflexión, ¿crees que todos estos edificios miden exactamente los valores recogidos aquí? ¿No variará ni un centímetro? ¿Tendría sentido recoger en esta infografía los posibles decimales? La respuesta probablemente sea no, ya que las diferencias entre unos y otros son de metros.

Imagen tomada de una infografía de Visual20. Licencia CC
Esto puede llevarnos a otro planteamiento... ¿existe un orden de aproximación establecido de antemano para hacer una aproximación? La respuesta es NO. Dependerá de lo que se desea medir. Así, carecería de sentido fijar el mismo orden de aproximación para medir la distancia entre dos ciudades o el diámetro de una pelota de tenis de mesa.
En el día a día no es necesaria mucha precisión, basta con 2 ó 3 decimales. Eso sí, la cosa cambia si manejamos datos científicos.
Importante
Se llaman cifras significativas a aquellas con las que se expresa un número aproximado. Solo debemos utilizar aquellas cuya exactitud nos conste.
Cuando realizamos una aproximación podemos hacerla por exceso o por defecto. Estos conceptos están más asimilados en nuestra vida cotidiana de lo que parece. Por ejemplo, la duración del año solar medio no contiene un número exacto de días, por lo que se hacen aproximaciones a la unidad, usando dos tipos de años: el de 365 días (aproximación por defecto) y el de 366 (año bisiesto, aproximación por exceso).
Hay distintos métodos de aproximación:
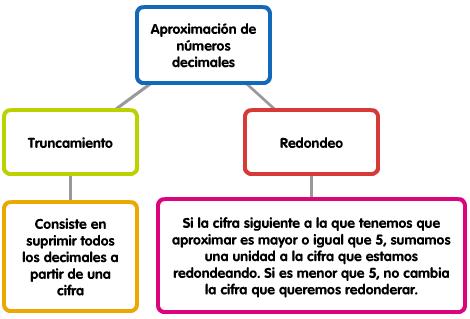
Imagen de elaboración propia
Comprueba lo aprendido
Completa la siguiente tabla:
Aproximación de raíces no exactas
En el tema anterior trabajamos con raíces exactas, pero ¿qué ocurre cuando el radicando no es un cuadrado perfecto? Podemos hacer una estimación de su valor recurriendo a los números decimales:
Vídeo de Yoestudio alojado en Youtube