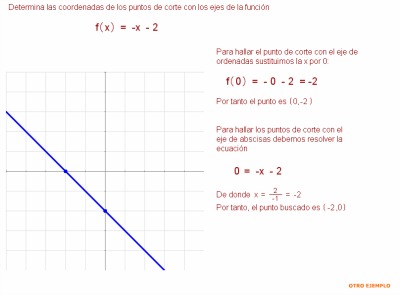
3.1. Dominio, simetría, cortes y asíntotas
|
| Fotografía en Flickr por Meet The Chumbeques bajo CC |
Vamos a comenzar el estudio completo de una función que desembocará en la representación gráfica de la misma. Pero antes hazte la idea de que eres un pintor profesional, y que estás a punto de realizar un trabajo que se te ha encargado. Supongo que si consigues meterte en situación, ya estarás pensado en tu lienzo y en el boceto. Pues bien, si es ese el caso ya estás listo para comenzar:
Dominio de una función. Tamaño del lienzo
El estudio del dominio de una función, va ligado a todas sus características. Influye en el estudio de la continuidad de la función y por lo tanto en las asíntotas, monotonía (crecimiento y decrecimiento)... Es por ello por lo que siempre es el primer paso que tenemos que dar.
¿Recuerdas cómo se calculaba el dominio de una función? Aunque suponemos que sí, para hacer memoria puedes ver el siguiente vídeo:
Si leíste en su momento las orientaciones del alumnado, quizás te llamara la atención la siguiente frase: "El orden y la claridad de exposición así como la capacidad de síntesis son factores que serán tenidos en cuenta [...]". Por eso es conveniente que te acostumbres a utilizar la notación adecuada en cada momento.
Importante
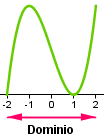
Imagen de elaboración
propia |
Notación
El dominio de una función se indica en forma de intervalo o entre llaves.
De esta forma, si una función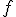 
tiene por dominio los puntos comprendidos entre 
y 
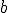(con 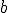no incluido), lo expresamos como 
.
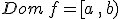Si usamos las llaves en vez de los corchetes o los paréntesis, dejamos de hablar de intervalos y nos referimos a puntos. Por ejemplo, si escribimos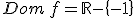 
entonces el dominio de nuestra función serán todos los números reales excepto el punto 
.
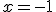Observa que para hablar de todos los números reales utilizamos la letra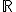 
(como ya vimos en la unidad 1).
Ejemplo o ejercicio resuelto
Consideramos la siguiente función racional: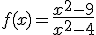 
Perseguimos realizar la representación gráfica de esta función. Para ello, en esta ocasión te pedimos que calcules el dominio de la misma.
Y ahora a trazar las primeras líneas y puntos.
Simetría de la función
Recuerda que otro de los aspectos que estudiamos de las funciones es la simetría.
Actividad
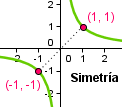
Imagen de elaboración
propia |
Una función es simétrica respecto al eje de ordenadas (OY), si para todo valor,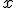 
, de su dominio se cumple que: 
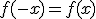. En este caso decimos que la función es Par.
Una función es simétrica respecto al origen de coordenadas, si para todo valor, 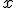, de su dominio se cumple que:
. En este caso decimos que la función es Impar.
Aunque existen funciones de los dos tipos descritos, Par e Impar, lo más frecuente es que una función no presente ningún tipo de simetría.
Puedes practicar con el siguiente applet de Descartes el concepto de función Par/Impar.
Escena de María José García Cebrian en Proyecto Descartes. Licencia CC
Ejemplo o ejercicio resuelto
Consideramos la siguiente función racional: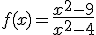
Te pedimos que estudies la simetría de la misma.
Puntos de corte con los ejes
Hay unos puntos que tienen especial interés, aquellos en los que la gráfica corta a los ejes de coordenadas.
Importante
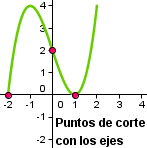
Imagen de elaboración
propia |
El punto de corte de la función con el eje vertical, el de ordenadas, es aquel en el que la variable se hace cero. Por lo tanto, basta anular la variable en la función para obtener la ordenada del punto de corte. Es decir, en la función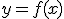 
será un punto de la forma 
.
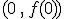Por su parte, el corte de la gráfica de la función con el eje de abscisas, el horizontal, corresponderá a un valor de 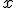que anule la función. Es decir, si se verifica que 
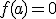, entonces el punto de corte con el eje horizontal será 
.
Si pinchas en la siguiente imagen puedes practicar el cálculo de los puntos de corte con los ejes de varias funciones, todas ellas correspondientes a líneas rectas.
Imagen de elaboración propia
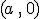Ejemplo o ejercicio resuelto
Consideramos la siguiente función racional: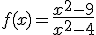
Calcula los puntos de corte con los ejes.
Asíntotas
El estudio de las asíntotas y ramas infinitas ya lo realizamos en el tema anterior junto con los límites de una función. Pero al ser una característica imprescindible para su representación, vamos a darle un pequeño repaso.
Si te fijas en las representaciones de rectas que hemos puesto como ejemplo durante estos temas nos hemos encontrado varias veces con ramas infinitas, es decir, tramos de curva que se alejan indefinidamente. Cuando una rama infinita se aproxima a una recta, a esta se le llama asíntota de la curva y a la rama correspondiente rama asintótica.
Importante
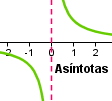
Imagen de elaboración
propia |
Dada una función 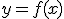cuya gráfica es la curva 
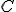se dice que la recta 
es una asíntota de 
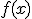si la curva 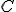se acerca a indefinidamente sin llegar a coincidir con la propia .
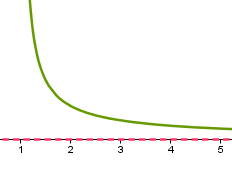
Como una asíntota es una recta, tenemos hasta tres posiciones distintas de una recta con relación a los ejes.
|
|
|
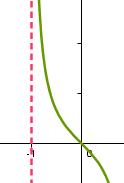
| A. Vertical |
A. Horizontal |
A. Oblicua |
Por ello, para cada función pueden existir hasta tres tipos distintos de asíntota.
La vertical existirá si el límite de la función tiende a infinito cuando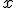
tiende a un valor finito , su valor será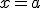 
.
La horizontal y la oblicua las encontraremos cuando estudiemos lo que ocurre cuando la variable independiente tienda a más o menos infinito.
En el caso de funciones racionales podemos hacer un estudio particular para saber qué tipos de asíntotas tendrán según sean el numerador y el denominador. Veámoslo en la siguiente presentación. Pulsa sobre la imagen para ir pasando de página.
Ejemplo o ejercicio resuelto
Dada la función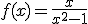 
, calcular sus asíntotas verticales y horizontales.
Ejemplo o ejercicio resuelto
Calcula la asíntota oblicua de las siguientes funciones:
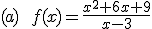
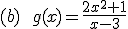
Para terminar un vídeo de juanmemol donde se estudian los tres tipos de asíntotas para una misma función.