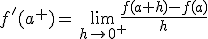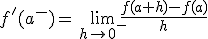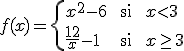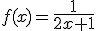2.1. Derivada en un punto. Función derivada
 |
| Fotografía en Flickr por taivasalla bajo CC |
Derivada en un punto
Como has visto en el vídeo anterior, el comportamiento estable de la variación media en el entorno de un punto permite definir “la tasa de variación instantánea” o lo que en lenguaje matemático se denomina derivada de la función en un punto.
Importante
Si tenemos una función 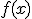 llamamos derivada de la función en un punto
llamamos derivada de la función en un punto 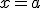 a la tasa de variación instantánea de la función
a la tasa de variación instantánea de la función 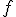 en el punto
en el punto  y se denota por
y se denota por 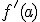 . Así, según la definición tenemos que:
. Así, según la definición tenemos que:
Recuerda que para que exista este límite, deben existir los límites laterales y coincidir. Así, de la misma forma, podemos definir las derivadas laterales como:
- Derivada por la derecha:
- Derivada por la izquierda:
En el caso de que ambos límites coincidan diremos que la función es derivable en el punto  .
.
Haciendo un simple cambio de variable 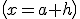 la derivada de
la derivada de 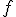 en un punto
en un punto 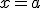 podemos expresarla también de la siguiente forma:
podemos expresarla también de la siguiente forma:
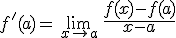
Importante
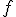 en
en 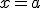 consiste en averiguar si la función es derivable en ese punto.
consiste en averiguar si la función es derivable en ese punto.
Caso de estudio
 |
Curso 2010/2011
(Continuación)
Estudie si la siguiente función es derivable en 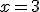 :
:
Interpretación geométrica de la derivada
Geométricamente, la derivada de una función en un punto es la pendiente de la recta tangente a la gráfica de la función en dicho punto, ya que las rectas secantes en el entorno de un punto tienden a confundirse con la recta tangente en el punto a medida que los incrementos se hacen más pequeños, como puedes descubrir en la siguiente animación:
Animación en INTEF de José Ángel López bajo CC
Caso de estudio
Halla la pendiente de la recta tangente a la gráfica
en el punto de abscisas 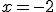 .
.
Función derivada
Dado que la derivada es un concepto local, podría definirse la función derivada en aquellos puntos en que la función primera o primitiva es derivable.
Actividad
Si tenemos una función 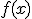 denominamos función derivada de
denominamos función derivada de 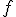 respecto a la variable
respecto a la variable 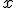 a una nueva función que para cada valor
a una nueva función que para cada valor 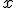 nos proporciona la derivada de la función en el punto
nos proporciona la derivada de la función en el punto 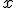 . A la función derivada de
. A la función derivada de 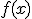 la denotaremos
la denotaremos 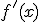 , aunque también la puedes ver representada como
, aunque también la puedes ver representada como ![]() . De esta forma tenemos que:
. De esta forma tenemos que:
Recuerda que con esta definición, la función derivada nos proporciona, para cada punto 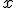 , la pendiente de la recta tangente a la función en punto
, la pendiente de la recta tangente a la función en punto 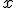 .
.
Caso de estudio
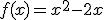
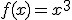 de la manipulación de su pendiente.
de la manipulación de su pendiente.
Applet de GeoGebra por Patricia Pérez