1.2. Función de probabilidad y de distribución

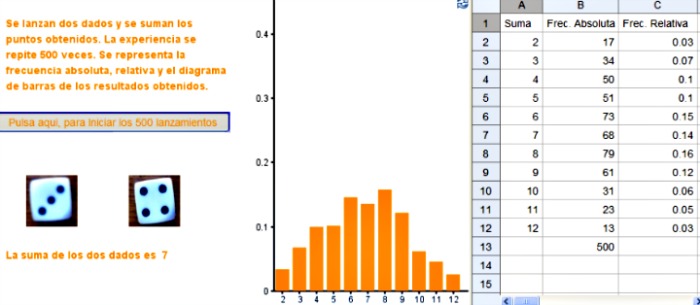
Si haces clic en la siguiente imagen puedes acceder a una escena de GeoGebra donde se simula el experimento aleatorio del lanzamiento de dos dados y sumar los puntos obtenidos. La experiencia se repite 500 veces, y se van viendo los lanzamientos, las variaciones de las frecuencias absolutas y relativas, y los cambios en el diagrama de barras que corresponde a las frecuencias relativas.

Captura de una escena de GeoGebra

Imagen de elaboración propia

Recuerda, la variable aleatoria relacionada con la experiencia anterior es la que asocia a cada lanzamiento de dos dados, la suma de puntos. Dicha variable 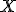toma los valores:

{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} 

que corresponde a los valores que pueden tomar las sumas.

En los 500 lanzamientos de la imagen anterior la suma 7 salió 68 veces, lo que le hace corresponder un frecuencia relativa de 0.14, en tanto que la suma 8 salió 79, por lo que tiene una frecuencia relativa de 0.16.

Pero los datos anteriores son solo 500 lanzamientos. Si repetimos la escena, saldrán otros valores distintos, pero a nosotros nos interesan las probabilidades teóricas asociadas a cada uno de los elementos de una variable aleatoria.

Importante

Llamaremos distribución de una variable aleatoria discreta 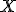al conjunto formado por los valores que toma 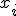y las probabilidades de que ocurran cada uno de ellos .

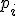Estas probabilidades, 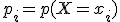, también reciben el nombre de función de probabilidad, y cumplen las siguientes propiedades:

  1. Son siempre positivas, es decir .

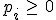  2. La suma de todas es igual a 1.

De la variable aleatoria del lanzamiento de dos dados, ya conocemos los 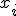(distintos valores que pueden tomar las sumas de los dos dados). Ahora tenemos que calcular la función de probabilidad, es decir, la probabilidad de que al lanzar dos dados, la suma de sus caras sea igual a : .

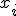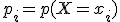Nos ayudaremos de la tabla siguiente.

  1
 2
 3
 4
 5
 6
 1  2 3 4 5 6 7
 2  3 4  5 6
7
 8
 3  4  5  6  7  8  9
 4  5  6  7  8  9  10
 5  6  7  8  9  10  11
 6  7  8  9  10  11  12

Aplicando la Ley de Laplace, casos favorables dividido entre casos posibles, obtenemos:

Valores de la variable
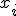 2
3
 4 5
6
7
8
9
10
11
12
 Frecuencias absolutas
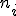 1
2
3
4
5
6
5
4
3
2
1
 Probabilidad  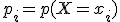 1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/26

Puedes comprobar que la suma de los 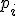es igual a 1, y evidentemente todos son mayores que 0.

Caso de estudio

Tres monedas
Imagen en Flickr de
Jason Rogers bajo CC

Realizamos el experimento aleatorio de lanzar tres monedas al aire, y definimos la siguiente variable aleatoria
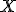= "número de caras que obtenemos".

Contesta a las siguientes cuestiones:

  1. Describe los valores 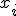que puede tomar la variable .

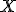  2. Determina el espacio muestral, E.

  3. Calcula la función de probabilidad, 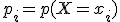, de la variable .

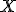Importante

En una variable aleatoria discreta 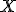, definiremos la función de distribución asociada a ella como

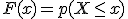
que asocia a cada número 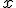, la probabilidad acumulada hasta él.

Las funciones de distribución de una variable aleatoria discreta son funciones definidas a trozos, donde los intervalos de definición de la función están comprendidos entre dos valores consecutivos de .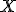

Por ejemplo, en el caso del lanzamiento de las tres monedas que hemos visto anteriormente, como 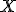= {0, 1, 2, 3}, los intervalos serán [0, 1), [1, 2), [2, 3) y [3, +∞).

  • En [0, 1) la función tomará el valor correspondiente a una probabilidad de que 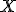sea menor que 1, es decir:

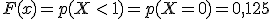
  • En [1, 2) la función sera igual a la probabilidad de que 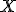sea menor que 2, es decir:

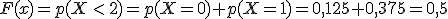
  • En [2, 3):

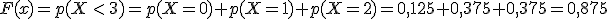
  • En [3, +∞):

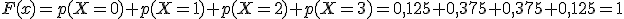
La gráfica y expresión analítica de la función serían las siguientes:

Gráfica y expresión analítica
Imagen de elaboración propia

Caso de estudio

Sea 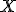una variable aleatoria discreta con la siguiente función de probabilidad.

   
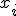
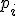0
  0.1
 1 
 0.2
 2 
 0.1
 3 
 0.4
 4 
 0.1
 5 
 0.1

a) Calcula y representa la gráfica de su función de distribución.

b) Halla las siguientes probabilidades: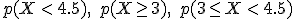

En el siguiente vídeo se hace un buen resumen de todos los conceptos estudiados hasta ahora de variable aleatoria. Está en gallego, pero se entiende con claridad.