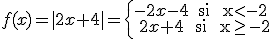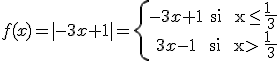2.3. Formalizamos el valor absoluto

Acabamos de ver cómo actúa el valor absoluto sobre la gráfica de una función. Vamos ahora a transformar el valor absoluto de una función en una función a trozos, y lo vamos a hacer sobre la más simple, sobre f(x) = |x|

Ya sabemos, que el valor absoluto deja lo positivo como positivo y lo negativo lo transforma en positivo.

Por tanto, si x es positivo (x>0) el valor absoluto de x seguirá siendo x, o sea, |x|=x

Por otro lado, si x es negativo (x<0) el valor absoluto de x lo cambiará de signo y será así -x, luego, |x|=-x

Y si x = 0, pues seguirá siendo 0 el valor absoluto, o sea, que igual lo podemos poner en cualquiera de las dos desigualdades.

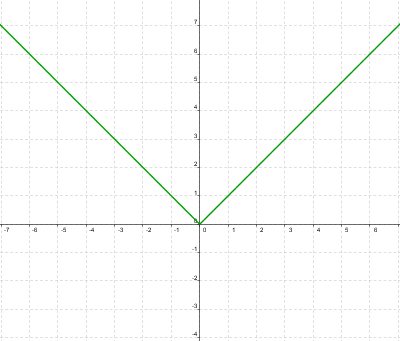
Si lo escribimos como una función a trozos, tendremos que:

y su gráfica será:

Gráfica de la función valor absoluto de x.

Ejemplo o ejercicio resuelto

Vamos a transformar en funciones a trozos las siguientes funciones que vienen dadas por valores absolutos:

La primera, f(x) = |2x+4|

Solution:

Aplicando lo mismo que antes, tendremos que la función vale lo mismo si 2x+4 es positivo y cambiada de signo si es negativo, es decir,

Ahora bien, 2x+4 < 0 equivale a decir que 2x < - 4, o lo que es lo mismo que x<-2. Por tanto, nuestra función queda así:

O de manera ordenada:

Una vez más, insistimos en que el signo = de la desigualdad da lo mismo donde se coloque, con el < o con el >.

Como segundo ejemplo, vamos a transformar en función a trozos la función y = |-3x + 1|

Solution:

Empezaríamos de la misma forma:

Y ahora, a ver a qué equivale -3x+1<0. Despejamos y nos queda -3x<-1 y pasando el -3 dividiendo, x>1/3. (Ojo, hay que recordar que cuando se dividía o se multiplicaba por un número negativo, la desigualdad cambiaba de sentido)

Así que nos queda:

Para saber más

Si tenemos otro tipo de función la forma de pasarla a trozos es similar. Únicamente varía la forma de transformar los dominios.

Por ejemplo, si tenemos y = |x² - 5x + 6|, empezamos igual:

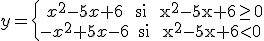
Ahora, para ver esa inecuación x²-5x+6<0, resolvemos la ecuación x²-5x+6=0 (aplicando la fórmula) y obtenemos como resultado 2 y 3.

Hacemos una tablita y vemos los signos de la función en cada intervalo:

(-∞, 2)	(2,3)	(3, + ∞)
+	-	+

Para completar los signos, le hemos dado un valor a x dentro de ese intervalo, lo hemos sustituido en la función y hemos visto el signo del resultado.

Entonces nuestra función a trozos queda:

AV - Reflexión

Transforma a trozos la función y = | 4x - 12 | y haz su gráfica.

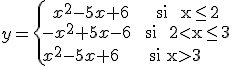
Para saber más

Si aún te ha quedado alguna duda sobre el valor absoluto, el siguiente vídeo repasa todo lo que debes saber sobre el valor absoluto y la función valor absoluto: