1. Gráficas de funciones elementales.
Actividad 1.-
Representa las gráficas de las siguientes funciones elementales:
$1) f(x)=-2x+3$
$2) f(x)=\large{\frac{-2x+3}{x+1}}$
$3) f(x)=\large{\frac{-x+3}{2x+1}}$
$4) f(x)=(-x+3)(2x+1)$
$5) f(x)=-x^2+7x-10$
$6) f(x)=2x^2+7x-9$
$7) f(x)=2^{2-x}+7$
$8) f(x)=\large{-2(\frac{4}{3})^{2x-4}}+3$
$9) f(x)=-2\ln(x-3)+3$
$10) f(x)=\ln(4x-2)-4$
Actividad 2.-
Determina las expresiones de las funciones siguientes, asociadas a sus respectivas gráficas:
Gráfica 2
Gráfica 3

Actividad 3.-
Sea la función $f(x)=e^x$. Se pide que determines la gráfica de las siguiente funciones transformadas a partir de la dada:
$a) f_1(x)=2f(x-2)+3$
$c) f_3(x)=-2f(x+2)-3$
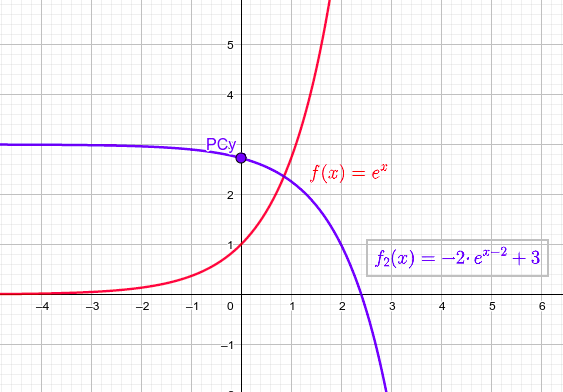
$b) f_2(x)=-2f(x-2)+3$
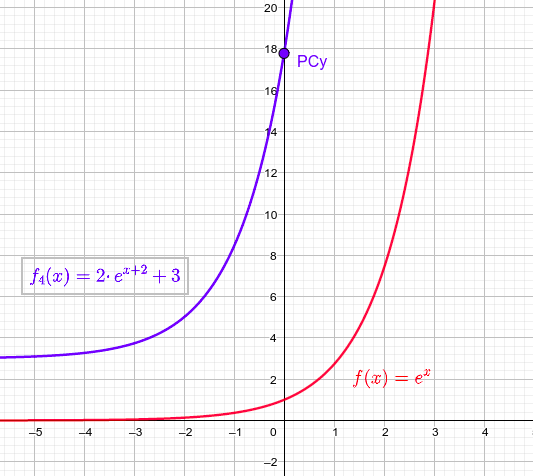
$d) f_4(x)=2f(x+2)+3$
Actividad 4.-
Determina los puntos de corte de las siguientes funciones con los Ejes de Coordenadas:
$a) f_1(x)=2e^{-x}+2$
$c) f_3(x)=2\ln (x-2)+2$
$b) f_2(x)=-2e^{2-x}+2$
$d) f_4(x)=-2\ln (x+2)-2$
Actividad 1
En esta actividad se trata de encontrar la gráfica de 10 funciones, pero lo primero es distinguir de qué tipo de función se trata. A lo largo del tema se han dado unas pautas claras para distinguir los diferentes tipos de funciones a partir de su expresión analítica, tal y como se nos muestran en este ejercicio.
Por tanto lo primero es darse cuenta de qué tipos de funciones tenemos:
- (1) es una recta, porque se trata de un polinomio de primer grado.
- (2) y (3) son hipérbolas por tratarse de expresiones racionales, cocientes de polinomios de primer grado, las funciones.
- (4), (5) y (6) son parábolas por tratarse de funciones que son polinomios de segundo grado. Hay que fijarse bien en que la (4), donde aparentemente no se observa el término de x², nos saldrá en el momento en que efectuemos el producto y multipliquemos -x por 2x.
- (7) y (8) son exponenciales porque tenemos la incógnita x en el exponente.
- (9) y (10) son logaritmos, estas se ven claras porque aparece la función ln.
Recordemos qué pasos debemos dar para representar cada una de ellas, porque en cada tipo, lo que necesitamos es diferente:
- Para la recta, nos basta con obtener dos puntos. Podemos dar dos valores a x y calcular f(x) que será la coordenada y del punto. Podemos dar los valores que queramos, aunque podríamos dar los valores cero a x e y, y con ello obtener los puntos de corte con los ejes cartesianos, que siempre es conveniente tenerlos:
- Si $x=0 \rightarrow y=f(0)=-2·0+3=3 \rightarrow PC_{y}:(0,3)$
- Si $y=0 \rightarrow 0=f(x) \rightarrow 0=-2x+3 \rightarrow 2x=3 \rightarrow x=\large{\frac{3}{2} } \rightarrow PC_{x}:\large{\left(\frac{3}{2},0)\right)}$
- Para las parábolas, según como tengamos la expresión, podemos sacar directamente determinada información tal y como se ha expuesto en el tema. Si cogemos una de las que están en forma general $f(x)=ax²+bx+c$ y trabajamos con ella, la (4) que no está así siempre, podremos efectuar y partir de su expresión general. Si no nos acordamos de extraer la información que lleva en esa forma:
- Lo primero es ver hacia donde se abre, si $a<0$ se abre hacia abajo, tendrá un máximo. Si $a>0$ se abre hacia arriba y tendrá un mínimo.
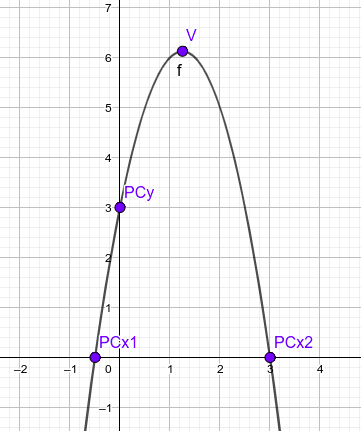
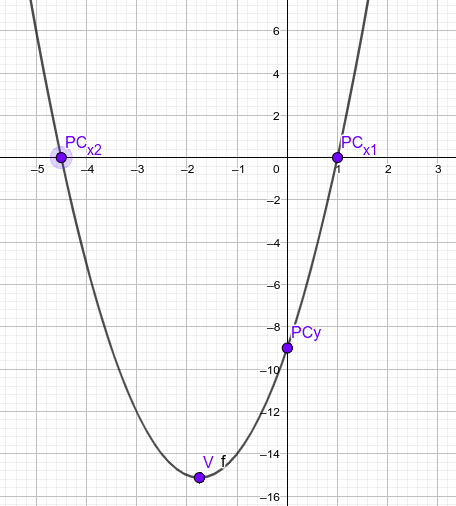
- Vamos a trabajar con la (6), en los otros dos casos se hará semejante y se deja como tarea, aunque al final se muestran todas las gráficas.
- El vértice es el punto más importante de la parábola, hay que encontrarlo para que el dibujo sea correcto. Hay varias formas de hacerlo, tal como se ha visto en el tema. Una de ellas es partir de la expresión en forma general y calcular sus coordenadas que están relacionadas con los valores a, b y c de la parábola:
- $x_{v}=-\large{\frac{b}{2a}}=-\large{\frac{7}{2·2}}=-\large{\frac{7}{4}}$
- $y_{v}=f(x_{v})=f \left(-\large{\frac{7}{4}}\right)=2·\left(-\large{\frac{7}{4}}\right)^{2}+7·\left(-\large{\frac{7}{4}}\right)-9=2·\large{\frac{49}{16}}-7·\large{\frac{7}{4}}-9=-\large{\frac{121}{8}}$
- Por tanto el vértice es el punto: $V:\large{\left(-\frac{7}{4},\large{-\frac{121}{8}}\right)}$
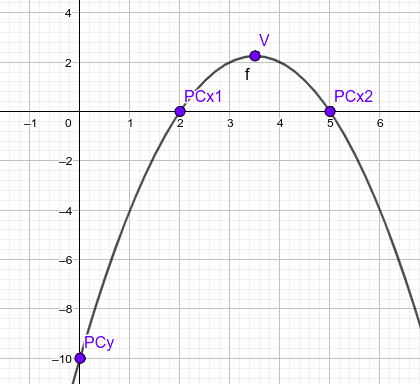
- Los puntos de corte con los ejes son los siguientes puntos más importantes de esta función. Se calculan exactamente igual que en cualquier función, dando el valor cero a x y calcular y para el punto de corte con el eje y. Después daremos el valor cero a y y calcularemos las x para los puntos de corte con el eje x:
- Si $x=0 \rightarrow y=f(0)=2·0^{2}+7·0-9=-9 \rightarrow PC_{y}:(0,-9)$
- Si $y=0 \rightarrow 0=f(x) \rightarrow 0=2x^{2}+7x-9$ Resolvemos la ecuación de segundo grado y obtenemos como resultados:
$x_{1}=1$ y $x_{2}=\large{-\frac{9}{2}}$ con lo que los puntos de corte con el eje x son: $PC_{x1}:(1,0)$ y $PC_{x2}:\large{\left(-\frac{9}{2},0\right)}$
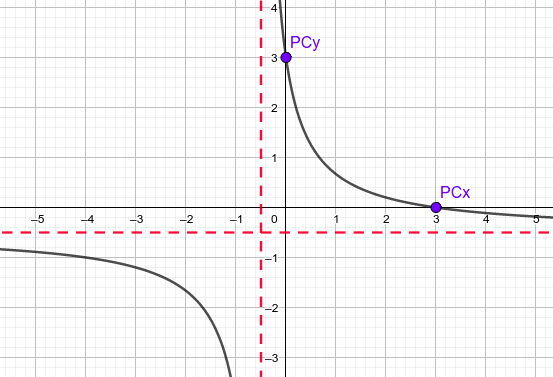
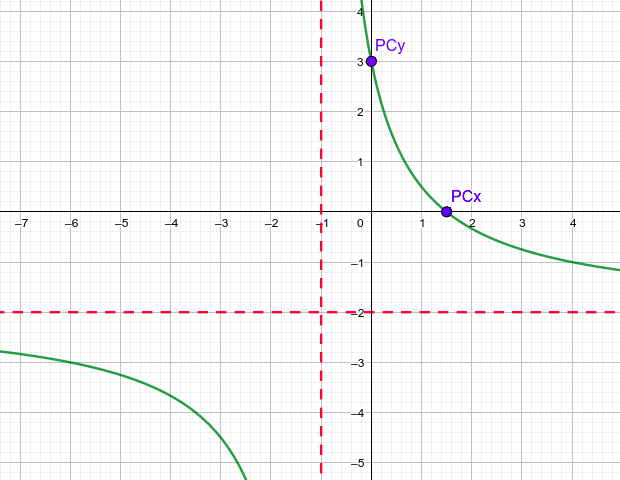
- Para las hipérbolas, como las tenemos con la expresión de cociente de polinomios de primer grado, podemos calcular las dos asíntotas y los puntos de corte con los ejes. Los puntos de corte se hacen igual que en todas las anteriores y las asíntotas, la vertical es la solución de igualar a cero el denominador y la horizontal es y igual al cociente de los coeficientes de las x del numerador y denominador. Vamos a estudiar y representar la función del ejercicio (2) y dejamos la (3) como tarea, aunque se muestra el dibujo de la gráfica al final:
- Puntos de corte:
Si $x=0 \rightarrow y=f(0)=\large{\frac{-2·0+3}{0+1}}=3 \rightarrow PC_{y}:(0,3)$
Si $y=0 \rightarrow 0=f(x) \rightarrow 0=\large{\frac{-2x+3}{x+1}} \rightarrow -2x+3=0 \rightarrow 2x=3 \rightarrow x=\large{\frac{3}{2} } \rightarrow PC_{x}:\large{\left(\frac{3}{2},0\right)}$ - Asíntotas:
Vertical: $\text{denominador}=0 \rightarrow x+1=0 \rightarrow x=-1$
Horizontal: $y=\text{cociente de coeficientes de x}=\large{\frac{-2}{1}}=-2 \rightarrow y=-2$
- Puntos de corte:
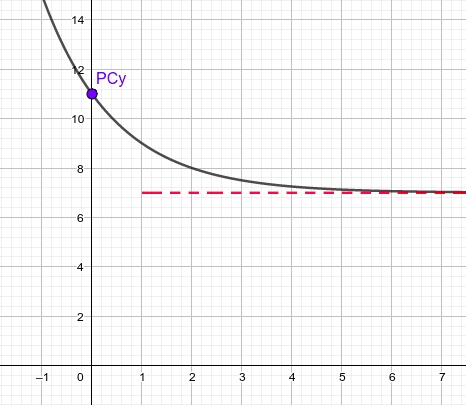
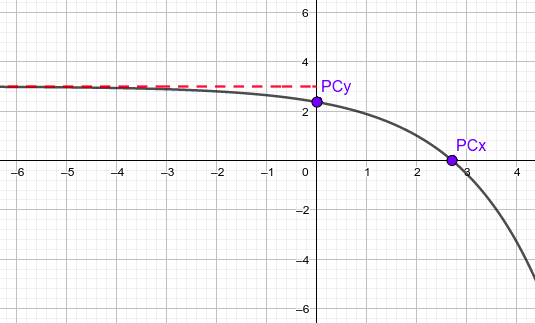
- Para las exponenciales lo primero que debemos hacer es expresarlas tal como la hemos estudiado en el tema, hemos de jugar con las operaciones para poder expresarlas en la forma: $f(x)=A·(\text{base})^{ax}+B$ porque la base no tiene por qué ser el número e. Igual que en los casos anteriores, haremos completa la función del ejercicio (8) y dejaremos la (7) para tarea.
- Vamos a reorganizar la expresión para hacerla semejante a esa función base de exponenciales, jugando con las operaciones:
$f(x)=-2·\large{\left(\frac{4}{3}\right)^{2x-4}}+3=-2·\large{\left(\frac{4}{3}\right)^{2x}}\div \large{\left(\frac{4}{3}\right)^{4}}+3=-2·\large{\left(\frac{4}{3}\right)^{2x}}\cdot \large{\left(\frac{3}{4}\right)^{4}}+3=$
$=2\cdot \large{\left(-\frac{81}{256}\right)}·\large{\left(\frac{4}{3}\right)^{2x}}+3=-\large{\frac{81}{128}}·\large{\left(\frac{4}{3}\right)^{2x}}+3$ - Entonces, una vez expresado así podemos estudiar las características tal como vimos en el tema, la base es mayor que uno pero el coeficiente A es negativo, por lo tanto los límites son:$ f(x)=-\large{\frac{81}{128}}·\large{\left(\frac{4}{3}\right)^{2x}}+3 \rightarrow \left\{ \begin{matrix} \text{Dominio}=\Re \\ \underset{n \to -\infty}{\lim} f(x)=3 \\ \underset{n \to +\infty}{\lim} f(x)=-\infty \end{matrix} \right. $
- Puntos de corte:
Si $x=0 \rightarrow y=f(0)=-\large{\frac{81}{128}}·\large{\left(\frac{4}{3}\right)^{2·0}}+3=-\large{\frac{81}{128}}+3=\large{\frac{303}{128}} \rightarrow PC_{y}:\large{\left(0,\frac{303}{128}\right)}$
Si $y=0 \rightarrow 0=f(x) \rightarrow 0=-\large{\frac{81}{128}}·\large{\left(\frac{4}{3}\right)^{2x}}+3 \rightarrow \large{\frac{81}{128}}·\large{\left(\frac{4}{3}\right)^{2x}}=3 \rightarrow \large{\left(\frac{4}{3}\right)^{2x}}=3·\large{\frac{128}{81}}=\large{\frac{128}{27}}$
$2x=\large{\ln_{\frac{4}{3}} \frac{128}{27} }\rightarrow x=\large{\frac{1}{2}}·\large{\ln_{\frac{4}{3}} \frac{128}{27} } \approx {\normalsize{2.70}} \rightarrow {\normalsize{PC_{x}:(2.70,0)}}$
- Vamos a reorganizar la expresión para hacerla semejante a esa función base de exponenciales, jugando con las operaciones:
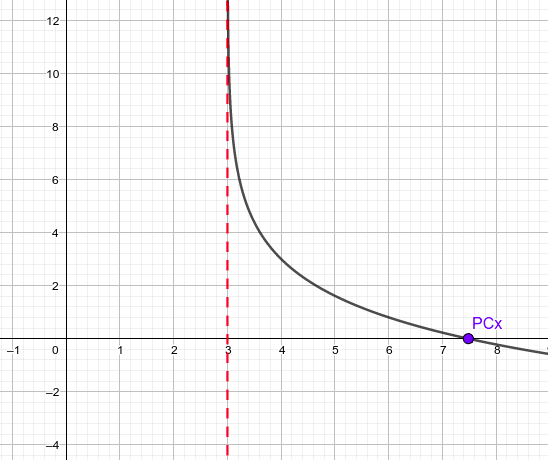
- En el caso de las logarítmicas, no hay que jugar tanto como en el caso de las exponenciales anteriores, ya tenemos las dos puestas de manera semejante a la expresión que vimos en el tema: $f(x)=A·\ln (ax+b) +B$. Vamos a estudiar completamente la (9) que tiene el valor de A negativo, en el caso de la (10) se hará de forma similar, y al final pondremos las gráficas de todos los casos, por tanto nuestra función será: $f(x)=-2· \ln(x-3) +3$
- El dominio de las funciones logarítmicas exige que el interior del mismo (argumento) sea positivo, por tanto debe cumplirse: $x-3>0 \rightarrow x>3$, con lo que el dominio de la función será: $\text{Dom} f(x)=(3,+\infty)$
- Al ser la base del logaritmo mayor que 1 ($e \approx 2,72$) debería ser creciente, pero como el coeficiente A es negativo y multiplica al valor del logaritmo, hace que el signo cambie y por tanto sea decreciente.
- Al comenzar su dominio a partir de x=3, no tiene sentido intentar buscar el punto de corte con el eje y, esta función no tiene corte con el eje y porque al sustituir x por cero nos quedaría el logaritmo de un número negativo que no es real.
- Para hallar el punto de corte con el eje x actuamos como siempre, pero tendremos que trabajar con la función recíproca pasando a exponencial:
Si $x=0 \rightarrow y=f(0)=-2·\ln(0-3)+3 \notin \Re \rightarrow PC_{y}:\text{No tiene}$
Si $y=0 \rightarrow 0=f(x) \rightarrow 0=-2·\ln(x-3)+3 \rightarrow 2·\ln(x-3)=3 \rightarrow \ln(x-3)=\large{\frac{3}{2} } \rightarrow (x-3)=e^{\large{\frac{3}{2} }}$ $x=e^{\large{\frac{3}{2} }}+3 \approx 7.48 \rightarrow PC_{x}:(7.48,0)$
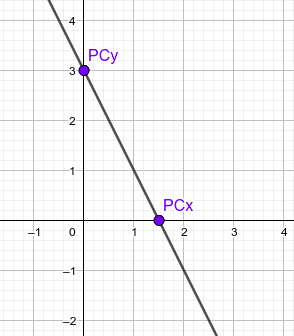
Finalmente se muestran las diez gráficas con sus características estudiadas:
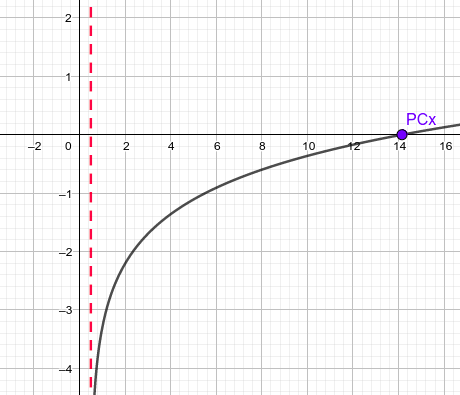
Actividad 2
Gráfica 1:
Datos observables:
- Se trata de una parábola, por lo que la expresión de la función tiene la forma: $f(x)=ax^{2}+bx+c$ donde tendremos que encontrar los valores de a, b y c.
- a debe ser positivo porque la parábola se abre hacia arriba.
- Tiene su vértice en el punto $V:(1,3)$ y pasa por el punto $A:(2,5)$
Con estos datos debemos calcular a, b y c:
Por simetría de la propia parábola podemos darnos cuenta de que el punto de corte con el eje y es el punto $PCy:(0,5)$, esto es así porque dos puntos que tengan su coordenada x a la misma distancia del valor de x del vértice deben tener el mismo valor de la coordenada y, y desde $x=1$ hasta $x=2$ hay la misma distancia que desde $x=1$ hasta $x=0$.
Por tanto debe cumplirse que $f(0)=5 \rightarrow a·0^{2}+b·0+c=5 \rightarrow c=5$
Por otra parte, sabemos que la coordenada x del vértice está relacionada con a y b: $x_{v}=\large{\frac{-b}{2a}}$ con lo que: $1={\large{\frac{-b}{2a}} }\rightarrow -b=2a \rightarrow 2a+b=0$
Finalmente, como pasa por el punto V, debe verificarla y ponemos ya que c es 5: $f(1)=3 \rightarrow a·1^{2}+b·1+5=3 \rightarrow a+b=-2 $
Resolvemos el sistema: $ {\Large{\left. a+b=-2 \atop 2a+b=0 \right \} }}\text{ } \underrightarrow{{\small{\text{ restando }}}}\text{ } a=2\text{ } \underrightarrow{{\small{\text{ sustituyendo }}}}\text{ } 2+b=-2 \rightarrow b=-4 $
Con lo que la expresión correcta de la función queda: $f(x)=2x^{2}-4x+5$
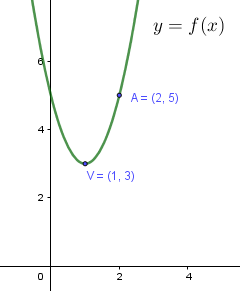
Gráfica 2:
Datos observables:
- Se trata de una hipérbola, por lo que la expresión de la función tiene la forma: $f(x)={\large{\frac{ax+b}{cx+d}}}$
- Tenemos además tres datos: Asíntota vertical: $x=-1$; asíntota horizontal: $y=-3$ y pasa por el punto $(1,-2)$
Aparentemente nos faltaría un dato porque tenemos cuatro parámetros a calcular a, b, c y d y solo tres datos, pero no es cierto porque la propia división relaciona también todos los datos. El proceso a seguir es el siguiente:
Expresamos el denominador de la manera más sencilla que verifique que la solución de la ecuación de primer grado resultante de igualar a cero es la asíntota vertical, osea:
$x+1$ porque al igualarlo a cero obtenemos la expresión de la asíntota vertical. También valdrían expresiones como $2x+2$ ó $7x+7$ pero lógicamente vamos por la más simple.
Con esto hemos obtenido los valores de c y d: $c=1$ y $d=1$.
El valor de la asíntota horizontal coincide siempre en una función de este tipo con el cociente de los coeficientes de x de ambos polinomios de primer grado, con lo que se debe cumplir:
$-3={\large{\frac{a}{c}}}$ y como $c=1$ obtenemos a: $-3={\large{\frac{a}{1}}} \rightarrow a=-3$
Ya solo basta verificar el punto conocido para obtener b, que es la que nos falta:
$f(x)={\large{\frac{-3x+b}{x+1}}} \rightarrow f(1)=-2 \rightarrow {\large{\frac{-3·1+b}{1+1}}}=-2 \rightarrow -3+b=-4 \rightarrow b=-1$
Con lo que definitivamente la función es: $f(x)={\large{\frac{-3x-1}{x+1}}}$
Gráfica 3:
Datos observables:
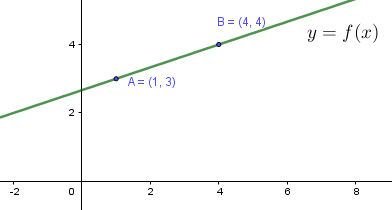
Se trata de una línea recta, por lo que la expresión de la función tiene la forma: $f(x)=ax+b$. Solo necesitamos dos puntos conocidos para hacer un sistema y calcular los valores de a y b
Tenemos dos puntos que nos da la gráfica: $A:(1,3)$ y $B:(4,4)$
El sistema quedaría:
$ {\Large{\left. 4a+b=4 \atop a+b=3 \right \} }}\text{ } \underrightarrow{{\small{\text{ restando }}}}\text{ } 3a=1 \rightarrow a={\large{\frac{1}{3}}}\text{ } \underrightarrow{{\small{\text{ sustituyendo }}}}\text{ } b=3-{\large{\frac{1}{3}}} \rightarrow b={\large{\frac{8}{3}}} $
Por lo que la expresión de la función será: $f(x)={\large{\frac{x+8}{3}}}$
Gráfica 4:
Datos observables:
- Se trata de una línea recta, por lo que la expresión de la función tiene la forma: $f(x)=ax+b$. Solo necesitamos dos puntos conocidos para hacer un sistema y calcular los valores de a y b
- Tenemos dos puntos que nos da la gráfica: $A:(2,2)$ y $B:(1,3)$
El sistema quedaría:
$ {\Large{\left. 2a+b=2 \atop a+b=3 \right \} }}\text{ } \underrightarrow{{\small{\text{ restando }}}}\text{ } a=-1\text{ } \underrightarrow{{\small{\text{ sustituyendo }}}}\text{ } -1+b=3 \rightarrow b=4 $
Por lo que la expresión de la función será: $f(x)=-x+4$
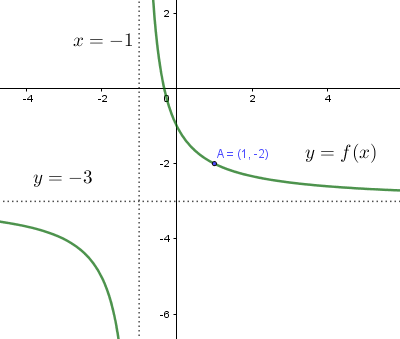
Gráfica 5:
Datos observables:
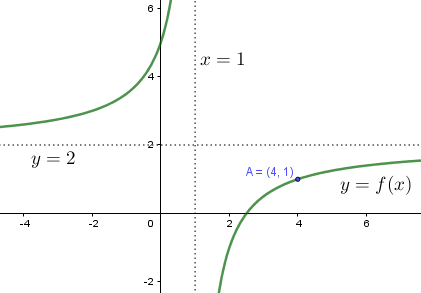
Se trata de una hipérbola, por lo que la expresión de la función tiene la forma: $f(x)={\large{\frac{ax+b}{cx+d}}}$
Tenemos además tres datos: Asíntota vertical: $x=1$; asíntota horizontal: $y=2$ y pasa por el punto $(4,1)$
Igual que en el caso anterior, el proceso a seguir es el siguiente:
Expresamos el denominador de la manera más sencilla que verifique que la solución de la ecuación de primer grado resultante de igualar a cero es la asíntota vertical, osea:
$x-1$ porque al igualarlo a cero, obtenemos la expresión de la asíntota vertical. Recordad que también valdrían expresiones como $2x-2$ ó $7x-7$ pero lógicamente vamos por la más simple.
Con esto hemos obtenido los valores de c y d: $c=1$ y $d=-1$.
El valor de la asíntota horizontal coincide siempre en una función de este tipo con el cociente de los coeficientes de x de ambos polinomios de primer grado, con lo que se debe cumplir:
$2={\large{\frac{a}{c}}}$ y como $c=1$ obtenemos a: $2={\large{\frac{a}{1}}} \rightarrow a=2$
Ya solo basta verificar el punto conocido para obtener b que es la que nos falta:
$f(x)={\large{\frac{2x+b}{x-1}}} \rightarrow f(4)=1 \rightarrow {\large{\frac{2·4+b}{4-1}}}=1 \rightarrow 8+b=3 \rightarrow b=-5$
Con lo que definitivamente la función es: $f(x)={\large{\frac{2x-5}{x-1}}}$
Gráfica 6:
Datos observables:
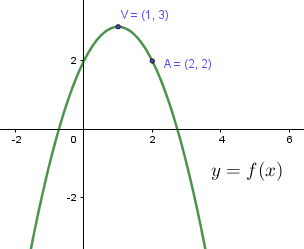
Se trata de una parábola por lo que la expresión de la función tiene la forma: $f(x)=ax^{2}+bx+c$ donde tendremos que encontrar los valores de a, b y c.
a debe ser negativo porque la parábola se abre hacia abajo.
Tiene su vértice en el punto $V:(1,3)$ y pasa por el punto $A:(2,2)$
Con estos datos debemos calcular a, b y c:
Por simetría de la propia parábola, podemos darnos cuenta de que el punto de corte con el eje y es el punto $PCy:(0,2)$. Esto es así porque dos puntos que tengan su coordenada x a la misma distancia del valor de x del vértice, deben tener el mismo valor de la coordenada y, y desde $x=1$ hasta $x=2$ hay la misma distancia que desde $x=1$ hasta $x=0$.
Por tanto debe cumplirse que $f(0)=2 \rightarrow a·0^{2}+b·0+c=2 \rightarrow c=2$
Por otra parte, sabemos que la coordenada x del vértice está relacionada con a y b: $x_{v}=\large{\frac{-b}{2a}}$ con lo que: $1={\large{\frac{-b}{2a}} }\rightarrow -b=2a \rightarrow 2a+b=0$
Finalmente, como pasa por el punto V, debe verificarla y ponemos ya que c es 2: $f(1)=3 \rightarrow a·1^{2}+b·1+2=3 \rightarrow a+b=1 $
Resolvemos el sistema: $ {\Large{\left. a+b=1 \atop 2a+b=0 \right \} }}\text{ } \underrightarrow{{\small{\text{ restando }}}}\text{ } a=-1\text{ } \underrightarrow{{\small{\text{ sustituyendo }}}}\text{ } -1+b=1 \rightarrow b=2 $
Con lo que la expresión correcta de la función queda: $f(x)=-x^{2}+2x+2$
Actividad 3
Se tratan de modificaciones sobre la función exponencial de tres maneras:
- Sumando o restando a la variable x en el exponente. Recordemos que eso desplaza la función hacia la derecha si se resta, o a la izquierda si se suma.
- Sumando o restando a la propia función, desplaza la función completa elevando cuando se suma, o bajando cuando se resta.
- Multiplicando la exponencial por un número, multiplica cada valor de la coordenada y del punto original por ese número.
- Si el número que multiplica es positivo, no afecta a los valores de los límites en los infinitos ni a la monotonía.
- Si es negativo, afecta al límite en el que la función se va a menos infinito o a más infinito cambiando su signo y además modifica la monotonía de toda la función, transformando el crecimiento de la función exponencial básica en decrecimiento.
Vamos a ver primero cómo quedan en cada modificación las expresiones analíticas y después veremos esas características comparando con la función exponencial básica. También vamos a incluir cómo quedaría el punto de corte con el eje y, que por el producto con el coeficiente que tiene delante se va a ver afectado, recordemos que la función $y=e^{x}$ corta al eje y en el punto: $(0,1)$:
- Función exponencial básica:
$ f(x)=e^{x} \rightarrow \left\{ \begin{matrix} \text{Dominio}=\Re \\ PC_{y}:(0,1) \\ \underset{n \to -\infty}{\lim} f(x)=0 \\ \underset{n \to +\infty}{\lim} f(x)=+\infty \end{matrix} \right. $
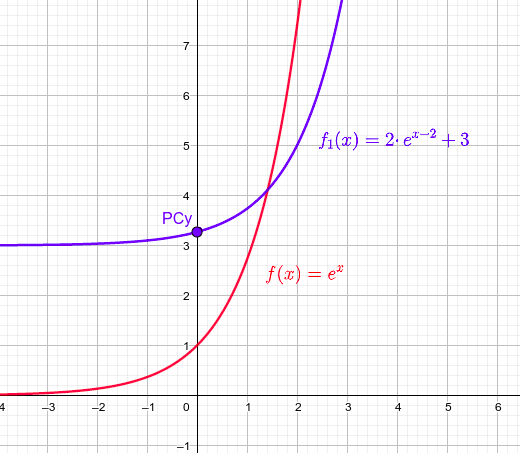
$ f_{1}(x)=2·e^{x-2}+3$
$\rightarrow \left\{ \begin{matrix} \text{Dominio}=\Re \\ PC_{y}:{\large{\left(0, \frac{2}{e^{2}}+3\right) }} \approx (0,3.27) \\ \underset{n \to -\infty}{\lim} f_{1}(x)=3 \\ \underset{n \to +\infty}{\lim} f_{1}(x)=+\infty \end{matrix} \right. $
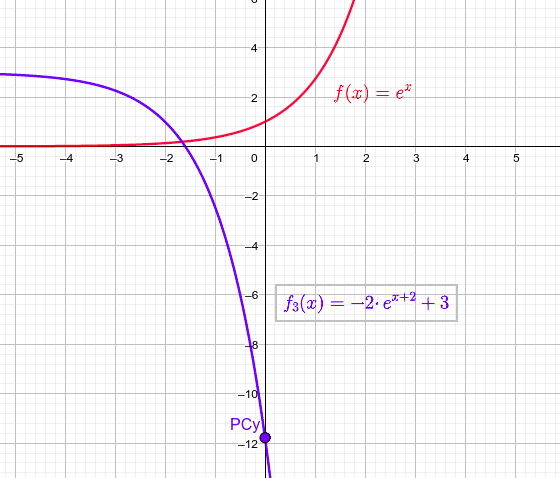
$ f_{3}(x)=-2·e^{x+2}+3$
$\rightarrow \left\{ \begin{matrix} \text{Dominio}=\Re \\ PC_{y}:\left(0,-2·e^{2}+3\right) \approx (0,-11.78)\\ \underset{n \to -\infty}{\lim} f_{3}(x)=3 \\ \underset{n \to +\infty}{\lim} f_{3}(x)=-\infty \end{matrix} \right. $
$ f_{2}(x)=-2·e^{x-2}+3$
$\rightarrow \left\{ \begin{matrix} \text{Dominio}=\Re \\ PC_{y}:{\large{\left(0, \frac{-2}{e^{2}}+3\right) }} \approx (0,2.73) \\ \underset{n \to -\infty}{\lim} f_{2}(x)=3 \\ \underset{n \to +\infty}{\lim} f_{2}(x)=-\infty \end{matrix} \right. $
$ f_{4}(x)=2·e^{x+2}+3$
$\rightarrow \left\{ \begin{matrix} \text{Dominio}=\Re \\ PC_{y}:\left(0,2·e^{2}+3\right) \approx (0,17.78)\\ \underset{n \to -\infty}{\lim} f_{4}(x)=3 \\ \underset{n \to +\infty}{\lim} f_{4}(x)=+\infty \end{matrix} \right. $
Finalmente, representaremos las cuatro gráficas por separado para que se vean bien los cambios. Dejaremos la función básica en rojo en cada uno de ellos para que se puedan comparar las modificaciones sufridas por la función original al realizar esos cambios.
Actividad 4
Como en cualquier función, para obtener los puntos de corte con los ejes cartesianos hay que hacer siempre lo mismo. Para el punto de corte con el eje y, sustituir x por cero y calcular el valor de la función, que será la coordenada y, si existe. Y para el punto, o los puntos de corte con el eje x (que puede haber más de uno), hay que sustituir la coordenada y por cero (o f(x)=0) y resolver la ecuación resultante. Vamos a hacer eso en cada una de las funciones:
Función 1: $f_{1}(x)=2·e^{-x}+2$
Punto de corte con el eje x: $y=0 \rightarrow 2·e^{-x}+2=0 \rightarrow 2·e^{-x}=-2 \rightarrow e^{-x}=-1 \rightarrow \text{No es real} \rightarrow \text{No corta al eje x} $
Punto de corte con el eje y: $x=0 \rightarrow y=f(0)=2·e^{-0}+2=2·1+2=4 \rightarrow PC_{y}=(0,4)$
Función 2: $f_{2}(x)=-2·e^{2-x}+2$
Punto de corte con el eje x: $y=0 \rightarrow -2·e^{2-x}+2=0 \rightarrow 2·e^{2-x}=2 \rightarrow e^{2-x}=1=e^{0} \rightarrow 2-x=0 \rightarrow x=2 \rightarrow PC_{x}=(2,0)$
Punto de corte con el eje y: $x=0 \rightarrow y=f(0)=-2·e^{2-0}+2=-2·e^{2}+2 \approx -12.78 \rightarrow PC_{y}=(0,-12.78)$
Función 3: $f_{3}(x)=2·\ln(x-2)+2$
Punto de corte con el eje x: $y=0 \rightarrow 2·\ln(x-2)+2=0 \rightarrow 2·\ln(x-2)=-2 \rightarrow \ln(x-2)=-1 \rightarrow x-2=e^{-1} \rightarrow x=2+e^{-1} \rightarrow PC_{x}=(2.37,0)$
Punto de corte con el eje y: $x=0 \rightarrow y=f(0)=2·\ln(0-2)+2 \rightarrow \text{No es real} \rightarrow \text{No corta al eje x} $
Función 4: $f_{4}(x)=-2·\ln(x+2)-2$
Punto de corte con el eje x: $y=0 \rightarrow -2·\ln(x+2)-2=0 \rightarrow 2·\ln(x+2)=-2 \rightarrow \ln(x+2)=-1 \rightarrow x+2=e^{-1} \rightarrow x=-2+e^{-1} \rightarrow PC_{x}=(-1.63,0)$
Punto de corte con el eje y: $x=0 \rightarrow y=f(0)=-2·\ln(0+2)-2 \rightarrow y=-2·ln(2)-2 \approx -3.39 \rightarrow PC_{y}=(0,-3.39) $