1.2. Perímetro y área
¿Qué es el perímetro de una figura plana?
La palabra perímetro, al igual que otras palabras relacionadas con las matemáticas, se utiliza en un lenguaje cotidiano. Observa la siguiente noticia:

Captura de pantalla del elpais.com
Ya hemos visto que un polígono está encerrado por una línea poligonal cerrada. Lo mismo ocurría con el círculo y la circunferencia. Si medimos esta línea poligonal o la longitud de la circunferencia estamos calculando el perímetro de la figura plana.

Imagen de intographics en Pixabay. Licencia CC
Importante
El perímetro de una figura plana, en el caso de los polígonos, es la suma de las longitudes de sus lados.
El perímetro de un círculo sería la longitud de la circunferencia (L). Se calcula con la fórmula: L=2∏r, donde r es el radio.
Ejercicio Resuelto
Si tomamos una cuerda de 0,5 metros y queremos hacer con ella un círculo de radio 5 cm y un pentágono regular de lado 3 cm, ¿tendremos suficiente?
¿Qué es el área de una figura plana?
El perímetro de una figura encierra una porción del plano cuya superficie podemos calcular. Al valor de la superficie de esa porción del plano de le conoce como área de ese plano o figura.
Importante
El área de una figura corresponde a la medida de la superficie que ocupa dicha figura.
Para saber el área de una figura plana, recurrimos a distintos métodos según el tipo de figura con la que nos encontremos.
Cálculo por fórmulas
Por ejemplo, para los triángulos, trapecios, paralelogramos y polígonos regulares tenemos fórmulas que nos ayudan a calcular el área de la figura, conociendo sus elementos característicos. En la siguiente imagen puedes ver las principales:
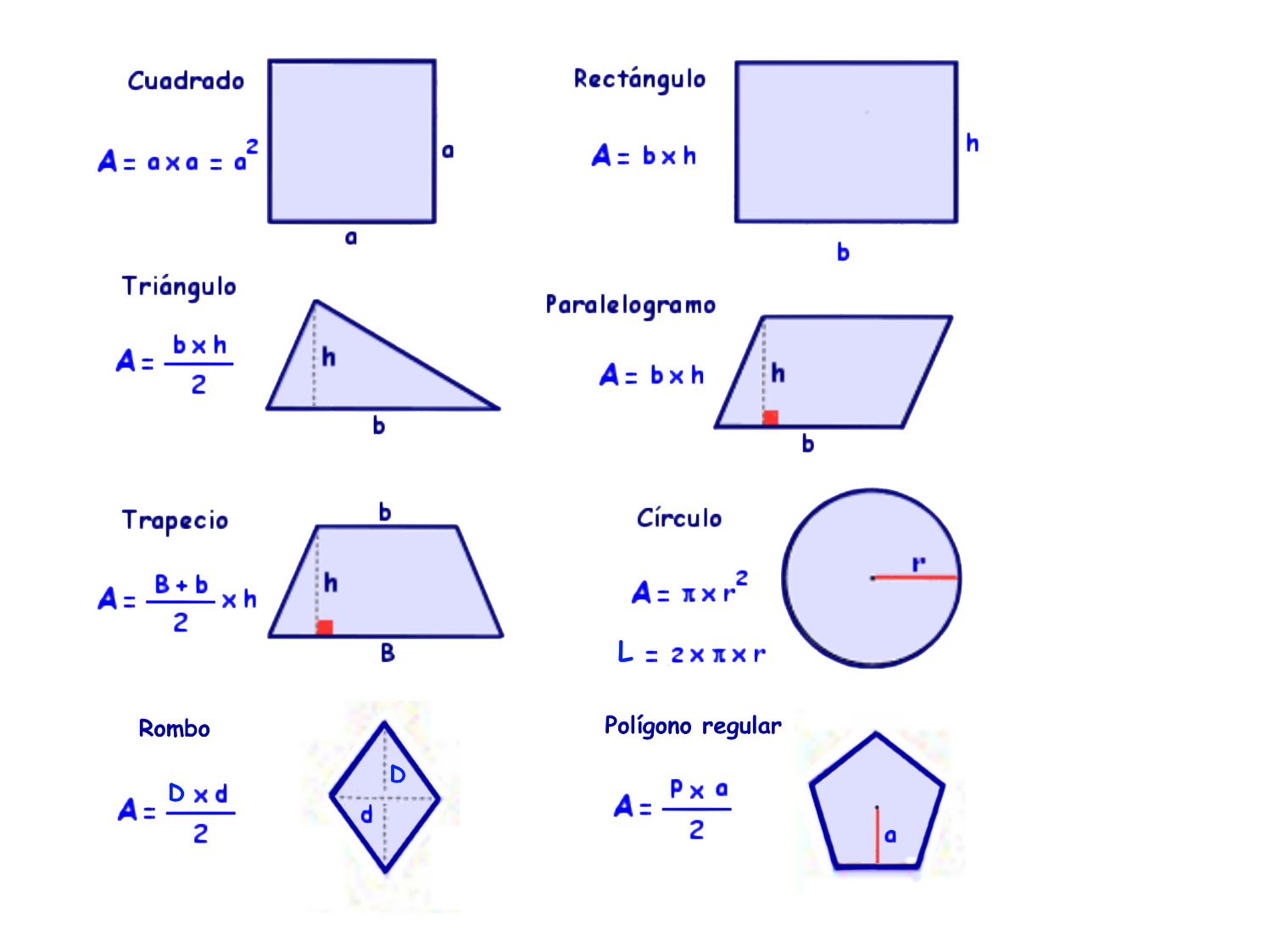
Imagen de Rodrigo en Geogebra.org. Licencia CC
Cálculo de áreas por descomposición
Cuando nos encontramos con un polígono irregular, para calcular el área recurrimos a la descomposición en figuras más simples y conocidas. Mira el siguiente ejemplo:
Escena de Josep Maria Navarro Canut Proyecto Descartes. Licencia CC
Comprueba lo aprendido
Practica el cálculo del área de los polígonos más habituales. Cuando hayas acabado uno pulsa en "otro ejercicio".
Comprueba lo aprendido
Indica si las siguientes afirmaciones son verdaderas o falsas:
Retroalimentación
Verdadero
El perímetro del hexágono regular sería 6·2=12
Su área es ![]()
Retroalimentación
Falso
El área del rectángulo es base por altura. Luego si tiene 5 m de base y 2,3 de altura el área tendría que ser 5·2,3=11,5 m2
Retroalimentación
Verdadero
La figura puede descomponerse en dos rectángulos y un triángulo:

El área del rectángulo amarillo seria 8 cm2, la del rectángulo naranja 4 cm2y la del triángulo 2 cm2. Entre las tres hacen un total de 14 cm2.
Curiosidad
Triangulación
Cualquier polígono puedes descomponerse en triángulos, sea cual sea su forma y por tanto, independientemente del tipo de polígono.
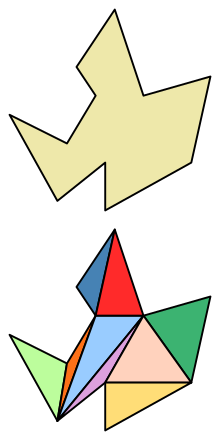 |
.svg.png) |
|
Imagen de Magistermathematicae en Wikimedia Commons. Licencia CC |
Imagen de Eric Détrez en Wikimedia Commons. Licencia CC |
Para ello solo tenemos que unir vértices no consecutivos. Un polígono de n-vértices, se puede descomponer en n triángulos, y hay distintas maneras de hacerlo.