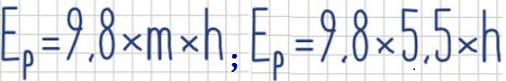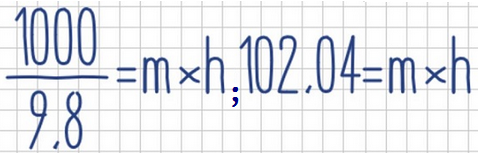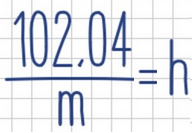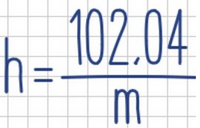4.2. Analizando datos de energía potencial gravitatoria
 |
| Imagen en Pixabay. Dominio público |
Estos datos (como los de la tabla anterior) pueden representarse en una gráfica. Así se puede tener una información visual muy rápida de cómo se relacionan las magnitudes.
Vamos a representar los datos de la tabla asociada a la energía potencial de una persona de 55 kg que está escalando una montaña de 100 metros de altura.
Para ello, debemos calcular la energía potencial que tiene a distintas alturas. ¿Cómo podemos hacerlo? Debemos conocer la función que relaciona la energía potencial con la altura.
- Primero sustituimos los datos en la fórmula de la Energía potencial. El único dato fijo que tenemos es la masa, que es 55 kg. Nos quedaría:
|
Elaboración propia |
- Realizamos el producto 9,8 × 55 y obtenemos:
|
Elaboración propia |
Esta es nuestra función donde la altura (h) es la variable independiente y varía entre 0m y 100m. Esto se escribe así 0≤h≤100.
La energía potencial es (Ep) que varía dependiendo del valor que toma la altura. Es la variable dependiente.
| Imágenes de elaboración propia | |
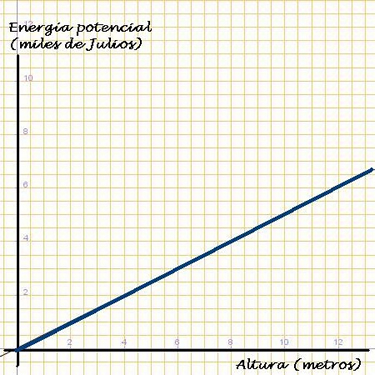
La gráfica que obtenemos es una línea recta que pasa por el origen de coordenadas.
Si observas los datos te darás cuenta de que:
- Si la altura se dobla, la energía aumenta también el doble.
- Si la altura se multiplica por 10, también la energía lo hace.
Recuerda: este tipo de relación entre dos magnitudes se llama relación lineal.
La gráfica corresponde a una función lineal. Este tipo de funciones ya las estudiamos con profundidad en el bloque 9.
Actividad
Recuerda: la representación gráfica de una relación lineal es siempre una recta que pasa por el origen de coordenadas.
 |
| Elaboración propia |
Cambiemos ahora de problema. Supongamos que ahora fijamos la energía potencial (del mismo modo que en el problema anterior fijamos la masa).
Supongamos que tenemos varios cuerpos, de masas comprendidas entre 10 y 100 kg, y queremos calcular a qué altura debe estar cada uno de ellos para tener una energía potencial de 1000 J.
Para no estar resolviendo constantemente la ecuación de primer grado cuya incógnita es "h", vamos a buscar la función donde la variable dependiente (la que va en eje vertical) es la altura y la variable independiente (la del eje horizontal) es la masa. La energía potencial está fija, 1000 J.
- Primero vamos a sustituir el valor de la energía potencial Ep=1000 J en la fórmula, con lo que nos quedaría:
|
Elaboración propia |
- Pasamos 9,8 dividiendo al lado izquierdo del = , y a continuación hacemos la división:
|
Elaboración propia |
- Ahora despejamos "h", ya que queremos que su valor dependa (sea dependiente) de la masa (m):
|
|
Elaboración propia
¡Y ya tenemos nuestra función!:
|
|
Elaboración propia
En esta función la masa varía entre 10 kg y 100 kg. Esto se escribe así 10≤m≤100
¿En qué se diferencia esta función de la anterior? La variable independiente m está elevada a 1 pero... ¡está en el denominador!
Vayamos a la tabla y fíjate en la gráfica que obtenemos:
| Elaboración propia | Elaboración propia |
Si observas los datos comprobarás que a más masa, se necesita menos altura para que la energía potencial sea constante. Más exactamente:
- Para el doble de masa, hace falta la mitad de la altura.
- Para 3 veces más masa hace falta 3 veces menos.
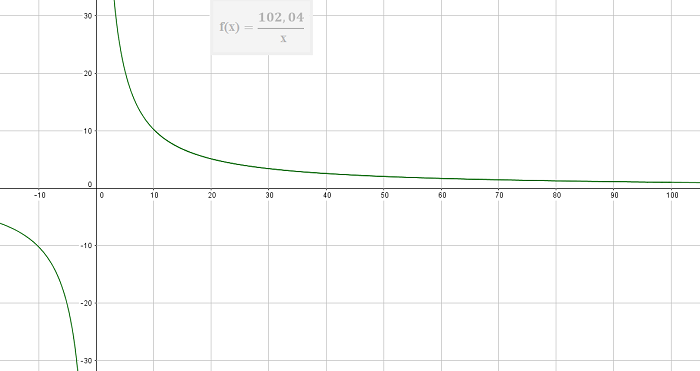
Este tipo de relación entre dos magnitudes se llama proporcionalidad inversa. En este caso decimos que la masa y la altura son inversamente proporcionales. La gráfica correspondiente es una curva decreciente, en forma de rama de hipérbola.
Objetivos
Para saber más…
Si quieres afianzar y/o profundizar sobre la función de proporcionalidad inversa puedes hacerlo con la siguiente lista de reproducción de vídeos del canal childtopia.
Ahora ya puedes practicar con la siguiente aplicación de GeoGebra.
La gráfica de la función del ejemplo anterior es un trozo de la gráfica de la función de proporcionalidad inversa, cuya fórmula y gráfica es:
 |
| Elaboración propia |