4. Perpendicular a dos rectas. Punto simétrico
 |
|
Imagen de elaboración propia
|
Seguro que cuando has estado paseando por algunas de las calles de tu ciudad has observado cables que cruzan de unos edificios a otros. Algunos pueden ser electricos, otros telefónicos.
Esas conexiones unen hilos de unas fachadas con otras Siempre están colocados de forma que la distancia que recorre por medio de la calle sea lo más corta posible, por lo tanto , suelen ser perpendiculares a las fachadas de las que salen.
En este apartado vamos a ver como calcular esas líneas que son perpendiculares a dos que ya tenemos.
Importante
 |
Si tenemos dos rectas, r y r', que se cruzan vamos a ver un método que nos va a permitir hallar la recta que corta perpendicularmente a las dos y la distancia entre las dos rectas. Ya comentamos en el apartado 1.1 que veríamos aquí como hallar esa distancia.
El proceso es el siguiente :
- Hallamos un punto genérico P de la recta r (que dependerá de su parámetro, por ejemplo, t).
- Hallamos otro punto Q genérico de la recta r' (dependerá de otro parámetro s).
- Calculamos el vector
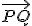, que dependerá de dos parámetros. - Imponemos que el vector anterior sea perpendicular a las dos rectas, r y r', y por lo tanto, los productos escalares por sus vectores de dirección deben dar cero.
- Nos queda un sistema de dos ecuaciones con dos incógnitas. Al resolverlo hallamos los valores de los parámetros t y s y por tanto los puntos P y Q que están sobre la perpendicular.
- Por último, la distancia entre las dos rectas que se cruzan es la distancia entre P y Q y la perpendicular común es la recta que pasa por P y Q.
Caso práctico
Dadas las rectas 
y 
.
Comprueba que se cruzan y halla la distancia entre las dos rectas y la perpendicular común a las dos rectas.
Si solo queremos hallar la recta que corta perpendicularmente a dos rectas que se cruzan, hay otro camino por el que podemos hacerlo. El proceso sería el siguiente.
- Hallamos un vector perpendicular a las dos rectas. Basta hallar el producto vectorial de los vectores dirección. Ese vector es el director de la recta buscada.
- Calculamos un plano que contenga a r y tenga el vector hallado antes como director.
- Determinamos otro plano que contenga a r' y al vector perpendicular hallado en el apartado 1.
- La recta buscada es la intersección de los dos planos hallados.
En la siguiente escena de geogebra puedes ver la recta perpendicular (en azul) a dos dadas (negro y rojo). Moviendo los puntos A y B puedes obtener nuevas rectas y su perpendicular correspondiente.
Caso práctico
Un arquitecto ha diseñado un edificio de 20 plantas. Por el suelo del sótano del edificio pasa un tubo que recoge el agua sucia del edificio y por el suelo de la azotea pasa un tubo que recoge toda el agua de lluvia. Este agua de lluvia debe llevarse a la tubería del sótano. Para llevarla, el arquitecto debe hacerlo por el trazado más corto. Para conseguirlo ha calculado con su programa de diseño gráfico la ecuación de la recta de la tubería de la azotea, resultando ser:
Tambien ha calculado la ecuación de la recta que sigue la tubería del sótano, resultando ser:
Sabe que ambas rectas se cruzan en el edificio, por lo que únicamente debe calcular la perpendicular común a las dos rectas. Intenta ayudarle.
Reflexión
Aplica todo lo aprendido en este apartado hallando la ecuación continua de la recta perpendicular a las rectas 
y 
. Calcula también la distancia entre las dos rectas.
Importante
 |
El punto simétrico de P respecto de un punto A es otro punto P' de forma que A sea el punto medio del segmento que une P y P'.
Ya en el tema 1 estudiamos las coordenadas del punto medio de un segmento. Por tanto, si conocemos las coordenadas de un punto 
y queremos hallar las coordenadas de su simétrico 
respecto de otro punto 
basta construir las ecuaciones siguientes y despejar las coordenadas de 
.
Como en partados anteriores, siempre que sea posible reduciremos nuevas situaciones a casos anteriores, como acabamos de hacer con el simétrico.
Así, para hallar el simétrico de un punto P respecto de una recta hallaremos el punto A que está sobre la recta dada y sobre la perpendicular a la recta por P, tal como vimos en el apartado 1.1, y después despejaremos las coordenadas del punto simétrico.
En la escena de abajo puedes ver el simétrico P´ (en rojo) de un punto P respecto a una recta. Moviendo el punto P por el espacio puedes hallar su nuevo simétrico respecto a la recta.
Caso práctico
 |
|
Imagen de elaboración propia
|
Es corriente que las grandes antenas de telefonía, de televisión, de electricidad cuando son simples, etc. lleven un anclaje al suelo mediante alambres de más o menos grosor, de forma que el viento no pueda hacerlas caer. Para que el anclaje sea más eficiente se suelen colocar las estacas de forma simétrica respecto a la antena, con el fin de que hagan fuerzas una frente a otra y fijen mejor la vertical de la antena.
Se va a colocar un gran repetidor de telefonía en una determinada situación y, mediante satélite, se está determinando la situación de sus anclajes. La antena se ha determinado que sigue la dirección de la recta 
. Si uno de los anclajes se situa en el punto 
, ¿en qué punto debería ir el simétrico?
Si queremos hallar el simétrico de un punto respecto de un plano procedemos como hicimos en el punto 1.2, hallando el pie de la perpendicular desde el punto exterior al plano, determinando así el punto medio del segmento formado por el punto y su simétrico.
En la siguiente escena puedes ver el punto simétrico P´ de P respecto a un plano. Moviendo tanto el punto P como el punto rojo del plano puedes ver como cambia el punto simétrico.
Rellenar huecos
Considera el punto 
y el plano 