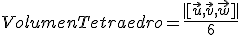2.2. Interpretación geométrica del producto mixto
Ya hemos analizado como podemos calcular áreas de un paralelogramo, la pregunta que nos hacemos ahora es ¿podemos calcular volúmenes ayudándonos de vectores? ¿Es posible calcular el volumen de un paralelepípedo gracias a los tres vectores que lo determinan?
Puedes observar que los paralelepípedos forman parte de nuestra vida diaria, desde una caja de zapatos, un mueble modular de un conocido fabricante Sueco de mobiliario o en construcciones arquitectónicas.
Aquí puedes apreciar algunos ejemplos de paralelepípedos.
 |
 |
|
|
Imagen en Flickr de Daniel Aguilar bajo licencia CC
|
Imagen en Flickr de Whicker Paradise bajo licencia CC |
Pre-conocimiento
En este video puedes conocer a Le Corbusier, un arquitecto frances que desarrolló su obra en la primera mitad del siglo XX y que demostró un especial amor por las matemáticas y las formas geométricas.
Actividad
 |
| Parallelepiped_volume.svg. Imagen obtenida de Wikipedia bajo licencia Creative Commons |
El área de la base formada por los vectores 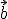 y
y 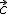 es
es 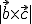 y el
y el 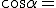
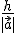 . Por lo tanto
. Por lo tanto
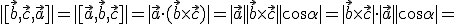
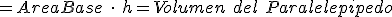
Ejemplo o ejercicio resuelto
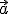 = (-1,1,2),
= (-1,1,2), 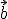 = (0,3,1) y
= (0,3,1) y 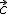 = (1,-1,3)
= (1,-1,3)
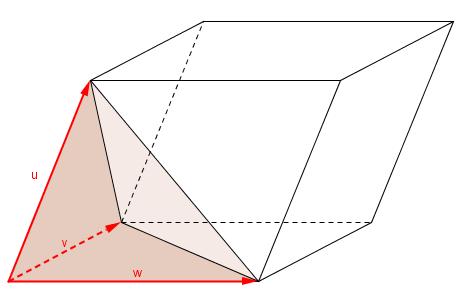
En el siguiente applet, puedes apreciar cómo tres vectores forman un paralelogramo y calcular el volumen formado por ellos.
El applet ha sido creado por Consolación Ruiz Gil, bajo licencia Creative Commons.
Actividad
El volumen del tetraedro es un sexto del volumen del paralelepípedo.