3.1. Término general
Te has parado alguna vez a pensar a que velocidad puede extenderse un rumor. Supongamos que Juan se entera de una información que le resulta interesante y se la comunica a 3 amigos a través de una red social tardando un minuto en ello. Posteriormente, estos 3 amigos la transmiten cada uno a otros tres en el siguiente minuto, y así sucesivamente. ¿Cómo evolucionaría el número de personas que tienen conocimiento de la información a lo largo del tiempo? La secuencia que obtenemos sería la siguiente: 1 (Juan), 3, 9, 27, 81, 243,... En cinco minutos, 243 personas estarían al tanto de la información. ¿Te sorprende esto? Los fenómenos que evolucionan de esta forma decimos que siguen una progresión geométrica.
Fotografía de LoboStudioHamburg en Pixabay. Licencia Pixabay
Importante
Se llama progresión geométrica a toda sucesión en la que cada término, exceptuando el primero, es el producto del anterior por una cantidad fija llamada razón.
Es decir,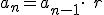 
, donde 
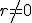es la razón y 
.
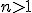En la progresión geométrica de los granos de trigo, la razón es 2 (un número mayor que 1 en valor absoluto). Esto implica que los términos de la progresión se van haciendo muy grandes en valor absoluto tal y como hemos podido comprobar con los granos que habría que poner en la casilla 64.
De igual forma, podemos considerar progresiones geométricas en las que la razón es un número menor que 1 en valor absoluto. Observa con detenimiento el siguiente vídeo:
Vídeo de tutomate alojado en Youtube
En la progresión geométrica anterior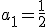 
, la razón es 
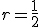y el término general es 
.
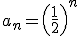Veremos más adelante cómo podemos calcular las sumas de las dos progresiones geométricas anteriores.
Al igual que ocurre con las progresiones aritméticas, existe una ley de formación para las geométricas.
Importante
Una progresión geométrica cuyo primer término es 
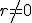y cuya razón es , tiene como término general:
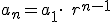
Ejercicio Resuelto
Halla los cinco primeros términos de una progresión geométrica de la que sabemos que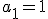 
y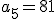 
.
Comprueba lo aprendido
Interpolar tres medios geométricos entre dos números a y b quiere decir intercalar tres números c, d y e entre a y b, de tal forma que los cinco números a, c, d, e y b formen una progresión geométrica.
Este problema se puede extender a interpolar cualquier cantidad de medios geométricos entre dos números conocidos. Por ejemplo, interpolar seis medios geométricos entre a y b quiere decir intercalar seis números entre ellos de tal forma que los ocho números, ordenados de menor a mayor, formen una progresión geométrica.
Para saber más sobre interpolación geométrica puedes ir a este enlace.
Ejemplo
Interpola tres medios geométricos entre 3 y 48.
Comprueba lo aprendido
A continuación, tienes algunos ejercicios para practicar con el término general de una progresión geométrica:
Escena de Miguel Ángel Cabezón Ochoa en Proyecto Descartes. Licencia CC