2.2. Suma de términos de una progresión aritmética

Recordemos a Gauss y su brillante idea para sumar los 100 primeros números naturales. ¿Podremos generalizarla para sumar los 200 primeros números? ¿O los n primeros?

Volvamos también a los números triángulares. ¿Cuántos puntos tendrá el que ocupa el lugar n?

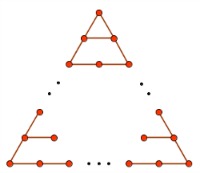Imagen de elaboración propia

Relacionemos las dos sucesiones anteriores. Por un lado tenemos la de los números naturales 1, 2, 3, 4... y, por otro, la de los números triangulares. Hagamos memoria:

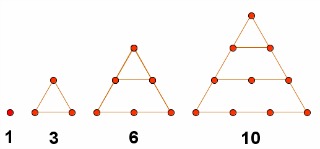Imagen de elaboración propia

Podemos ver que el número triangular que ocupa el lugar n es igual a la suma de los n primeros números naturales: 1 + 2 + 3 + ... + n.

Operando de forma similar a como lo hizo Gauss, tenemos:

	1	2	3	4	...	n-3	n-2	n-1	n
	n	n-1	n-2	n-3	...	4	3	2	1
Suma	n+1	n+1	n+1	n+1	...	n+1	n+1	n+1	n+1

Por tanto, dos veces la suma de los n primeros números naturales es igual al n·(n + 1). Esto quiere decir que la suma de los n primeros números naturales es igual a:

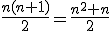
¿Será posible realizar un razonamiento similar para la suma de los primeros términos de cualquier progresión aritmética?

Comprobemos que sí en el siguiente vídeo:

Vídeo de tutomate alojado en Youtube

Importante

La suma de los 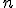primeros términos de una progresión aritmética de término general es igual a

Caso de estudio

Volvamos al número de asientos que tiene el patio de butacas del teatro Antonio Gala y que vimos en el apartado anterior. Recordemos que la primera fila tenía 20 asientos y que el resto de filas aumentaba en 2 asientos respecto a la que tiene delante.

Ahora nos preguntamos, ¿cuántos asientos hay en el patio de butacas si dispone de 15 filas en total?

Ejercicio Resuelto

Sabiendo que el primer término de una progresión aritmética es 30 y el cuarto es 39, halla la diferencia de la progresión y la suma de sus 25 primeros términos.