2.1. Término general
No solo los triángulos determinan un tipo de sucesión numérica. También es posible jugar con las letras del abecedario para generar sucesiones, por ejemplo, con la T.
 |
| Imagen de elaboración propia |
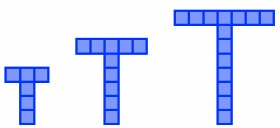
¿Cuántos cuadrados son necesarios para construir la primera T? ¿Y la segunda? ¿Y la tercera? ¿Y las sucesivas T?
En un principio parece que basta con contar los cuadrados: 6 para la primera, 10 para la segunda, 14 para la tercera... Pero si queremos conocer la regla de formación tendremos que fijarnos un poco más: 6 para la primera y, después, a cada nueva T se le añaden 4 cuadrados más.
Vamos a escribirlo utilizando la notación de sucesiones:
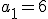 |
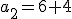 |
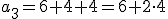 |
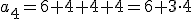 |
De lo anterior, podemos deducir que 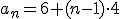 .
.
A este tipo de sucesiones se las denomina progresiones aritméticas.
Importante
Se llama progresión aritmética a toda sucesión en la que cada término, a excepción del primero, es la suma del anterior más una cantidad fija llamada diferencia.
Es decir 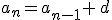 , donde
, donde  es la diferencia y
es la diferencia y 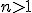 .
.
La sucesión anterior, la formada por los cuadrados necesarios para ir construyendo las sucesivas T, es una progresión aritmética en la que la diferencia vale 4.
Comprueba lo aprendido
Algunos de los ejemplos de sucesiones que hemos visto hasta ahora son progresiones aritméticas. Completa las siguientes afirmaciones.
Comprueba lo aprendido
Solución
En una progresión aritmética, si son conocidos su primer término y la diferencia, es posible conocer cómodamente cualquier término, es decir, es muy fácil determinar su término general.
Lo anterior ya lo hemos podido comprobar en el caso de los cuadros que hacen falta para ir formando las sucesivas T o con los múltiplos de 7.
En general, solo hace falta entender cómo se "comportan" los primeros términos de la progresión aritmética:
Vídeo de Tutomate alojado en Youtube
Importante
Una progresión aritmética cuyo primer término es  y cuya diferencia es
y cuya diferencia es  tiene como término general:
tiene como término general:
Caso de estudio
La primera fila del patio de butacas del teatro Antonio Gala de mi ciudad tiene 20 asientos mientras que el resto de filas aumenta en 2 asientos respecto a la que tiene delante.
¿Cuántos asientos tiene la fila que ocupa el lugar 15?
Ejercicio Resuelto
De una progresión aritmética se conocen los valores del segundo y del quinto términos, es decir, 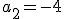 y
y 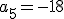 .
.
Determinar el término general de dicha progresión.
Comprueba lo aprendido
A continuación, tienes algunos ejercicios para practicar con progresiones aritméticas.
Escena de Miguel Ángel Cabezón Ochoa en Proyecto Descartes. Licencia CC
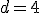 , por tanto
, por tanto 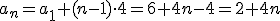 .
.