1.2. Monotonía y acotación

En biología se nos enseña que los seres vivos nacen, crecen, etc. En las sucesiones se pueden observar comportamientos parecidos.

Fotografía de Unsplash en Pixabay. Licencia Pixabay

Importante

Una sucesión a_n se dice monótona creciente cuando para todo y se dice estrictamente creciente cuando para todo .

Una sucesión a_n se dice monótona decreciente cuando para todo y se dice estrictamente decreciente cuando para todo .

Una sucesión a_n se dice alternada cuando el signo de a_n es distinto del de a_{n + 1} para todo .

Ejemplos

La sucesión a_n = n² es estrictamente creciente ya que (n + 1)² > n² para todo .
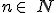La sucesión 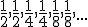es monótona decreciente pero no estrictamente decreciente.
La sucesión a_n = 4 es monótona creciente y monótona decreciente al mismo tiempo. Es decir, es constante.
La sucesión a_n = (-1)ⁿ es alternada ya que sus términos son -1, 1, -1, 1, -1, 1, ...

Falso

Obviamente, el enunciado es falso ya que, si tomamos, por ejemplo, la sucesión 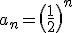comprobamos que sus términos disminuyen al aumentar el valor de n.

Una sucesión a_n se dice que es acotada superiormente cuando existe un número M llamado cota superior de la sucesión tal que para todo .

Una sucesión a_n se dice que es acotada inferiormente cuando existe un número m llamado cota superior de la sucesión tal que para todo .

Una sucesión a_n se dice que es acotada cuando es acotada tanto superior como inferiormente.

En la siguiente escena de Geogebra puedes visualizar la cota superior y la cota inferior de una sucesión.

Ejemplos

La sucesión a_n = 3 - n es una sucesión acotada superiormente y una posible cota superior es M = 3. Se puede comprobar también que no es acotada inferiormente.
La sucesión a_n = n² es una sucesión acotada inferiormente y una posible cota inferior es m = 0. Sin embargo, no es acotada superiormente pues dado un número M siempre podemos encontrar un número natural n tal que 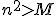, es decir, un número natural n que supere a esa supuesta cota superior M.
La sucesión 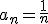es una sucesión acotada tanto superior como inferiormente en la que podemos tomar M = 1, m = 0.
La sucesión a_n = n · (-1)ⁿ no es acotada ni superior ni inferiormente.