1.1. Conceptos básicos
Importante
Una sucesión numérica es todo conjunto ordenado de números reales.
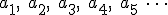
Cada uno de los elementos de la sucesión se llama término. Como puedes ver, utilizamos subíndices para conocer el lugar que ocupa cada término en la sucesión.
Se llama término general al que ocupa el lugar indeterminado 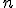 . Dicho término se expresa como
. Dicho término se expresa como  .
.
En muchas ocasiones, los términos de las sucesiones se pueden determinar a partir de cierto criterio. Este criterio se denomina regla de formación.
Como hemos visto en el apartado 1, sucesiones existen muchas y muy famosas como, por ejemplo, la sucesión de los números primos.
| Primer número primo | 1 |
| Segundo número primo | 2 |
| Tercer número primo | 3 |
| Cuarto número primo | 5 |
| Quinto número primo | 7 |
| Sexto número primo | 11 |
| Séptimo número primo |
13 |
El primer término de la sucesión, se simboliza como a1, el segundo como a2, y así sucesivamente, por lo que los primeros términos de la sucesión se denotarían como
a1 = 1, a2 = 2, a3 = 3, a4 = 5, a5 = 7, a6 = 11, a7 = 13, ...
Otra famosa sucesión es la formada por los cuadrados de los números naturales que, como ya habrás adivinado, tiene como primeros términos a1 = 1, a2 = 4, a3 = 9, a4 = 16, ... Esta sucesión tiene como término general an = n2. Gracias a esta expresión podemos determinar cualquier término de la sucesión, por ejemplo, para calcular el término quinto, tan solo sustituimos n por 5 y obtenemos a5 = 52 = 25.
Comprueba lo aprendido
Retroalimentación
Verdadero
Veamos los primeros términos de esta sucesión:
- a1 = 13 = 1
- a2 = 23 = 8
- a3 = 33 = 27
Comprueba lo aprendido
¿Te gustan los pasatiempos? En general, son pequeños divertimentos lógicos que nos hacen pensar y nos evaden durante cierto tiempo de la realidad. Veamos si eres capaz de resolver este que te proponemos:
Considera la siguiente secuencia numérica (los números que la forman son los llamados números triangulares).
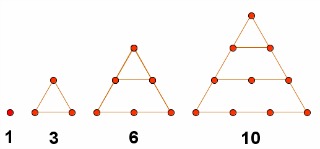 |
| Imagen de elaboración propia |
¿Sabrías decir cómo continúa la secuencia? ¿cuáles son el quinto y sexto número triangular? ¿y el décimo? ¿Serías capaz de dar una regla general para construirlos todos?
En el caso de números triangulares, tenemos que a1 = 1, a2 = 3, a3 = 6, a4 = 10, ...
Puedes comprobar que el término general de la sucesión formada por los números triangulares es 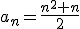 (Más adelante, en el apartado 2, veremos porqué).
(Más adelante, en el apartado 2, veremos porqué).
Vamos a verificar que esta expresión es cierta para el término que ocupa el segundo lugar: 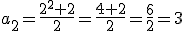 .
.
Esa expresión es la denominada regla de formación de los números triangulares, la cual nos permite conocer el valor de cualquier término sin más que conocer el lugar que ocupa en la sucesión. Por ejemplo, el término que ocupa el lugar 100 tendrá el valor 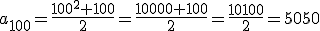 .
.
Ahora bien, no siempre es posible escribir el término general de una sucesión usando una expresión algebraica (aunque conozcamos la regla que sirve para hallar sus términos). Este es el caso de las sucesiones recurrentes, en las que cada término queda determinado si se conocen los dos términos anteriores.
La famosa sucesión de Fibonacci es de este tipo. Recuerda, a1 = 1, a2 = 1 y, a partir del tercer término, se cumple que an = an - 1 + an - 2, es decir, cada término se obtiene sumando de los dos términos anteriores.
Aplicando la regla de recurrencia anterior tenemos que:
- a3 = a2 + a1 = 1 + 1 = 2
- a4 = a3 + a2 = 2 + 1 = 3
- a5 = a4 + a3 = 3 + 2 = 5
- ...
Para saber más
Visualiza el siguiente vídeo sobre la sucesión de Fibonacci y la razón aurea:
Vídeo de Derivando alojado en Youtube
Comprueba lo aprendido
Recuerdas las tres primeras sucesiones que vimos al principio del tema:
- Los números naturales: 1, 2, 3, 4, 5...
- La tabla de multiplicar del 7: 7, 14, 21, 28, 35...
- Los cuadrados de los números naturales: 1, 4, 9, 16, 25...
Completa, a partir de ellas, las siguientes frases:
Comprueba lo aprendido
A continuación, tienes algunos ejercicios para practicar la obtención de algunos términos conociendo el término general:
Escena de Miguel Ángel Cabezón Ochoa en Proyecto Descartes. Licencia CC
