4.3. Asíntotas oblicuas
Actividad
Diremos que la función f(x) tiene una asíntota oblicua y su ecuación es y = mx + n si
 con
con 
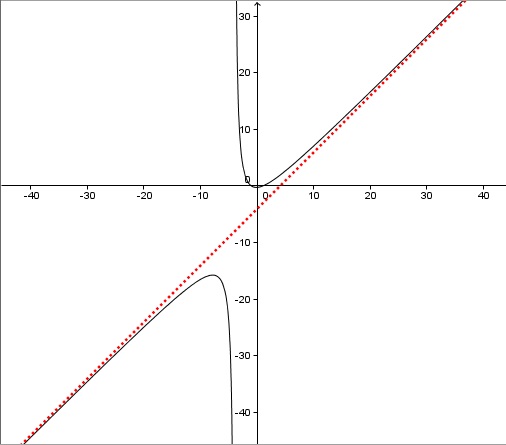
Dada la función 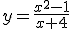 , vamos a proceder a calcular sus asíntotas oblicuas.
, vamos a proceder a calcular sus asíntotas oblicuas.
 En primer lugar determinaremos si realmente la función presenta una asíntota oblicua
En primer lugar determinaremos si realmente la función presenta una asíntota oblicua
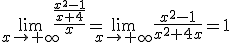
Por lo tanto existe una asíntota oblicua y la pendiente de dicha recta es 1. Determinemos ahora el valor de n
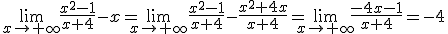
Por lo tanto la asíntota oblicua es y = x-4
El límite es análogo si 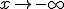
Caso de estudio
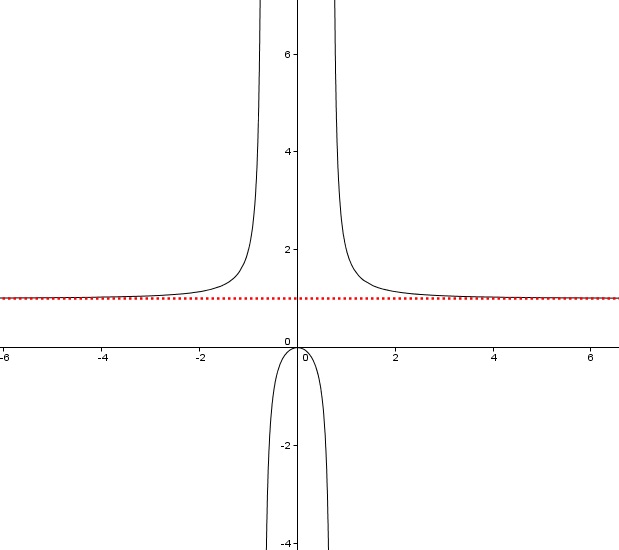
Analicemos un caso algo especial y es cuando al calcular una asintota oblicua, nos aparece una asíntota horizontal. Para ello, vamos a calcular las asíntotas oblicuas de la función 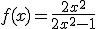 .
.
Actuamos como en los casos anteriores, calculando el límite de 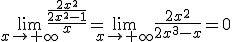 .
.
Así la pendiente de la asíntota oblicua es 0. Ahora pasamos a hallar el valor n de la asíntota oblicua.
 . Así la asíntotasería y =0·x+1=1, con lo que realmente, la función presenta una asíntota horizontal, no oblicua
. Así la asíntotasería y =0·x+1=1, con lo que realmente, la función presenta una asíntota horizontal, no oblicua
Pregunta de Elección Múltiple
Pregunta de Elección Múltiple
Pregunta Verdadero-Falso
Retroalimentación
Falso
La asíntota oblicua es y = x-2 . Veamos varios límites de este tipo y cómo se resuelven.
. Veamos varios límites de este tipo y cómo se resuelven.