2.3. Monotonía
Algunos términos matemáticos pueden llevar a confusión en su significado, ya que, algo monotono suele estar relacionado con situaciones tediosas y aburridas, algo que en absoluto queremos conseguir con este tema. Sin embargo, la monotonía no tiene porque ser aburrida, según la RAE, monotonía equivale a uniformidad, por lo que una diversión continua...también es monotona!
Actividad
Una función es monótona creciente si se cumple la siguiente condición,si
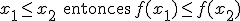
Diremos que es estrictamente creciente si
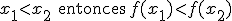
Actividad
Una función es monótona decreciente si se cumple la siguiente condición,si
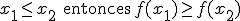
Diremos que es estrictamente decreciente si
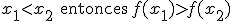
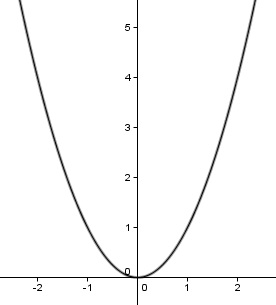
Estudiar la monotonía de una función, quiere decir, indicar los intervalos donde la función crece, decrece o es constante. Veamos un caso particular, la función x2.
Si analizamos graficamente la función, podemos indicar que la función decrece desde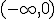 
, es decir, que tal como aumenta la variable x en dicho intervalo, la variable y cada vez es menor. Sin embargo en el intervalo 
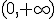,tal como crece la variable x, la variable y, crece por lo que la función es creciente.
Podemos concluir que el estudio de la monotonía de la función es el siguiente, la función x2 decrece en 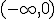y crece en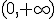
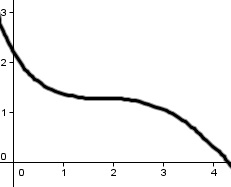
Caso de estudio
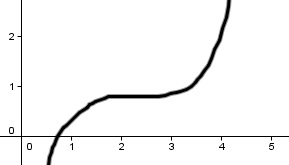
Analiza la monotonía de la función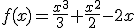 
cuya representación es la indicada. 
