2.2. Acotación. Máximos y mínimos absolutos y relativos.
El término cota es muy utilizado entre los aficionados al alpinismo, a la alta montaña o simplemente al trekking. Según la RAE, una de las acepciones de esta palabra es "Altura o nivel en una escala de valores", pero en matemáticas, también existe este término y tiene connotaciones muy parecidas. Antes de entrar en materia, puedes disfrutar de este video de las cotas mas significativas de Sierra Nevada
Actividad
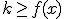 para cualquier valor de x que pertenezca al dominio de la función
para cualquier valor de x que pertenezca al dominio de la función
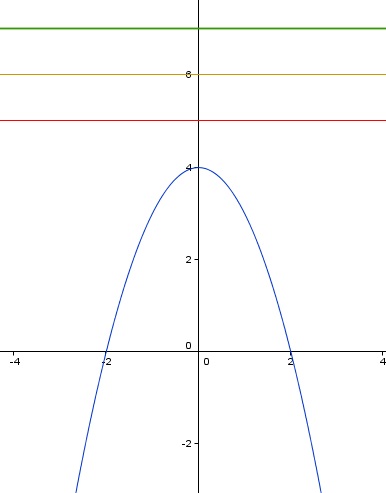
Analizamos la función f(x) = 4-x2. Sabemos que está función es de tipo cuadrática, por lo que su vértice se encuentra en 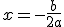 siendo la función y = ax2+bx+c, por lo que el vértice lo encoentramos en x= 0, con f(0) = 4. Por lo tanto, cualquier valor por encima de 4 es una cota superior de la función. Veamos graficamente la función y como los valores 5,6 ó 7 son cotas superiores.
siendo la función y = ax2+bx+c, por lo que el vértice lo encoentramos en x= 0, con f(0) = 4. Por lo tanto, cualquier valor por encima de 4 es una cota superior de la función. Veamos graficamente la función y como los valores 5,6 ó 7 son cotas superiores.
Actividad
 , donde x es cualquier núero que pertenece al dominio.
, donde x es cualquier núero que pertenece al dominio.
La función f(x) = x4 -2x2 + 2 tiene la siguiente representación gráfica
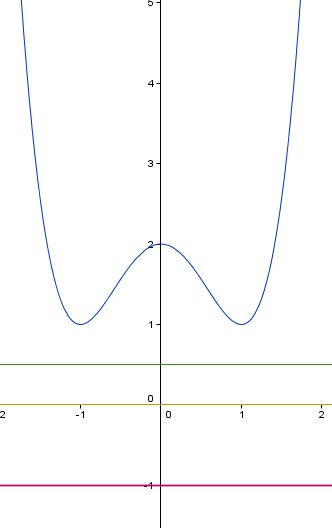
Por lo que podemos afirmar que las valores 0.5, 0 ó -1 son cotas inferiores de la función indicada
Actividad
Decimos que un valor a es el máximo absoluto de una función si pertenece al dominio y es la menor de las cotas superiores.
Analogamente decimos que un valor b es el mínimo absoluto de una función si pertenece al dominio y es la mayor de las cotas inferiores.
Estudiemos de nuevo la función f(x) = x4 -2x2 + 2, a la cual le calculamos varias cotas inferiores como 0.5 ó -1. Veamos esta nuevo imagen de la función.
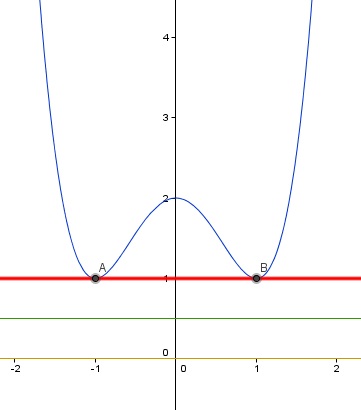
Vemos que el valor -1 es una cota de la función indicada y ademas es el mayor valor de las cotas inferiores, por lo que podemos asegurar que es el mínimo de la función. ¿Para qué valores de x alcanzamos esos valores? En este caso para dos valores. Si observas la gráfica, para los valores x= -1 y x= 1 alcanzamos el valor 1, es decir, f(1) = 1 y f(-1) = 1.
Para los valores x= 1 y x=-1 la función alcanza el mínimo y su valor es 1
Cabe preguntarnos una nueva cuestión ¿toda función tiene cota superior o inferior? ¿toda función tiene máximo o mínimo?
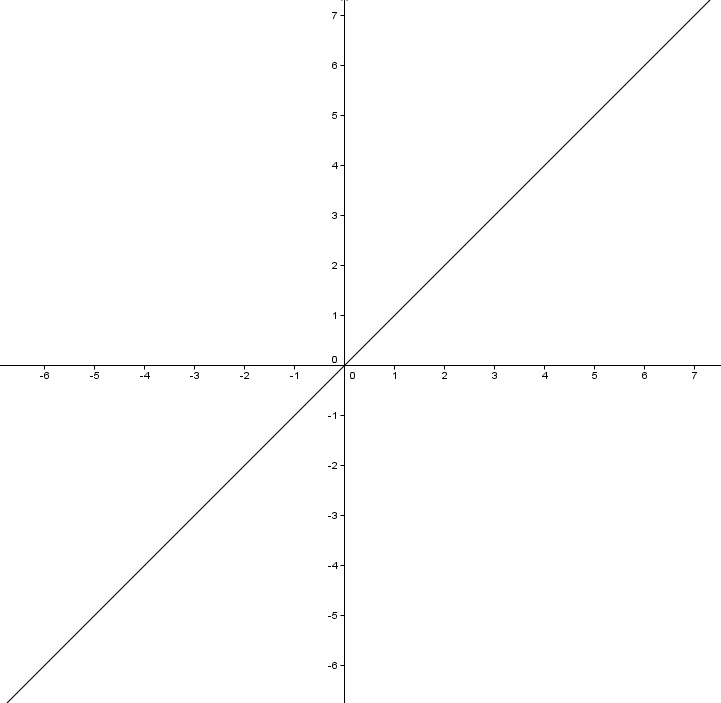
Analiza graficamente la función y = x y como puedes comprobar no existe ningún valor que sea superior o inferior a los valores de la función, por lo que podemos decir que existen funciones que no están acotadas y al no estarlo, por supuesto, no tienen ni máximo ni mínimo
Actividad
La función f(x) alcanza un máximo relativo en el punto a si f(a) es mayor o igual que las imágenes de los puntos cercanos a "a". Asi mismo, podemos decir que
la función f(x) alcanza un mínimo relativo en el punto b si f(b) es menor o igual que las imágenes de los puntos cercanos a "b".
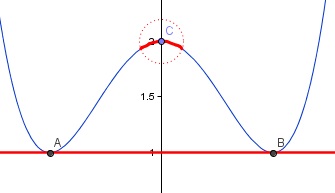
Volvemos a trabajar con nuestra ya vieja amiga función f(x) = x4 -2x2 + 2 y analicemos, viendo su gráfica, si tiene algún extremo relativo.
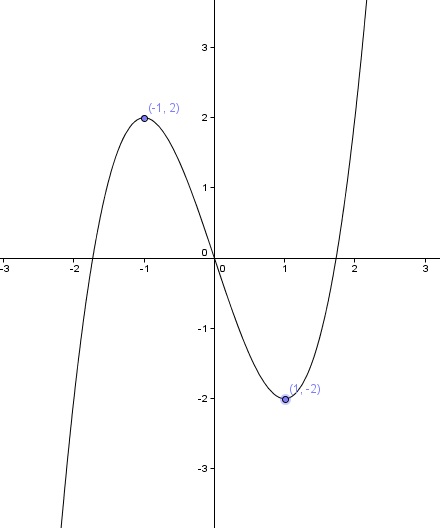
Vemos que para el valor de la función tomado para x=0. f(0)=2, es un máximo relativo, ya que en un entorno suyo, es el valor mas alto que toma la función. No globalmente, solo, como decimos, en un entorno de ella.
Caso de estudio
Determina las cotas, máximos absolutos y relativos de la función de la función f(x) = x3-3x, cuya representación es