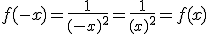2.1. Simetrías, funciones pares e impares.
Si queremos analizar una función y su gráfica, nos podemos encontrar situaciones en las que no es necesario estudiar todo el dominio de una función, simplemente estudiamos la mitad de su dominio. Es un ahorro considerable de esfuerzo!. l
En este video puedes apreciar la idea intuitiva de simetría
Actividad
Estudiemos desde dos puntos de vista la paridad de una función, desde la perspectiva gráfica y analítica.
GRAFICAMENTE
Estudiaremos si "doblando" el plano cartesiano por el eje Y, las gráfica coinciden. Veamos el caso f(x) = x2-4
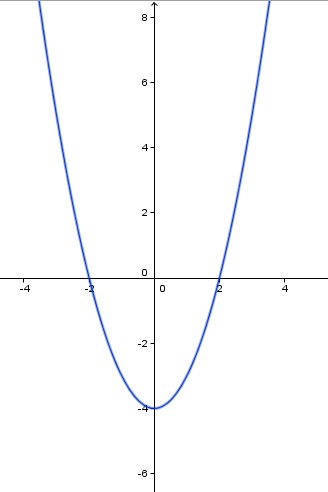
Visualmente, podemos decir que la función es par, ya que al "plegar" el plano, coincidirian las gráficas. La pregunta que nos podemos hacer es "¿realmente coinciden?"
Para asegurarno que es par, utilizaremos el método analítico
ANALITICAMENTE
Para comprobar si la función es par, aplicaremos la definción de paridad, es decir f(x) = f(-x)
Para ello, usustituimos en la función x por -x yapreciamos si la nueva función coincide con la incial
f(-x) = (-x)2-4 = (-1)2(x)2-4 = 1x2-4=x2-4. Esta función coincide con la inicial, por lo que f(-x) = f(x) y afirmaremos que la función es par.
CONCLUSIONES
A la hora de representar una función par, tan solo estudiaremos los valores mayores que 0 , ya que la representación para los valores menores coincidirá con la anterior.
Caso de estudio
Analiza la paridad de la función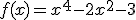 
Pregunta Verdadero-Falso
Retroalimentación
Falso
Aplicando la definción de paridad llegamos a lo siguiente
f(-x) = (-x)3+1 = -x3+1 que no coincide con f(x). Por lo tanto la función no es par.
Actividad
De forma análoga al caso de las funciones pares, estudiaremos la funciones impares.
Graficamente
Las funciones impares serán aquellas funciones que al girarlas 180º respecto del origen de coordenadas, coinciden con la original.
La representación de la función f(x) = x3-x es la siguiente
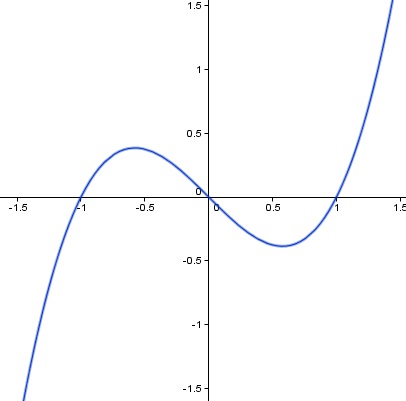
Apreciamos que si giramos la gráfica 180º coincide con la original. Otra interpretación de las funciones impares es que si "doblamos" el plano por el eje Y y posteriormente por el eje X, la gráfica coincide.
Analiticamente
Al igual que en el caso de la paridad, con el analisis gráfico podemos tener una idea si es impar la función, pero el único método fiable, es la aplicación de la definición. Veamos si f(x) = -f(-x)
Calculemos en primer lugar f(-x)
f(-x) = (-x)3-(-x) = (-1)3(x)3-(-x) =-x3+x
Determinamos ahora -f(-x)
-f(-x) = - (-x3+x) = x3-x
Coincide f(x) con -f(-x), por lo que podemos decir que f(x) es imar.
Caso de estudio
Determina si la función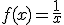 
es impar
Pregunta Verdadero-Falso
Retroalimentación
Falso
La función f(-x) coincide con f(x), por lo que la función no es impar, de hecho, es una función par.
