Las funciones matemáticas son herramientas poderosas para modelar procesos de la vida cotidiana, ayudando a entender y predecir comportamientos y resultados.

Observa el siguiente ejemplo: "Cálculo del costo de un viaje en taxi".

Supongamos que un taxi cobra una tarifa base (bajada de bandera) de 3 euros, más 2 euros por cada kilómetro recorrido.

Este escenario se puede modelar con una función lineal, donde el costo total del viaje es una función de la distancia recorrida.

La función matemática sería:

\[C(d) = 3 + 2·d\]

donde $C$ es el costo total en euros y $d$ es la distancia recorrida en kilómetros.

Si mostramos la gráfica de esta función, veremos una línea recta que comienza en el punto $(0, 3)$ en un gráfico de costo contra distancia. Esto significa que incluso si no recorres ninguna distancia $(d=0)$, todavía tendrías que pagar la tarifa base de 3 euros. A partir de ahí, el costo aumenta linealmente con la distancia.

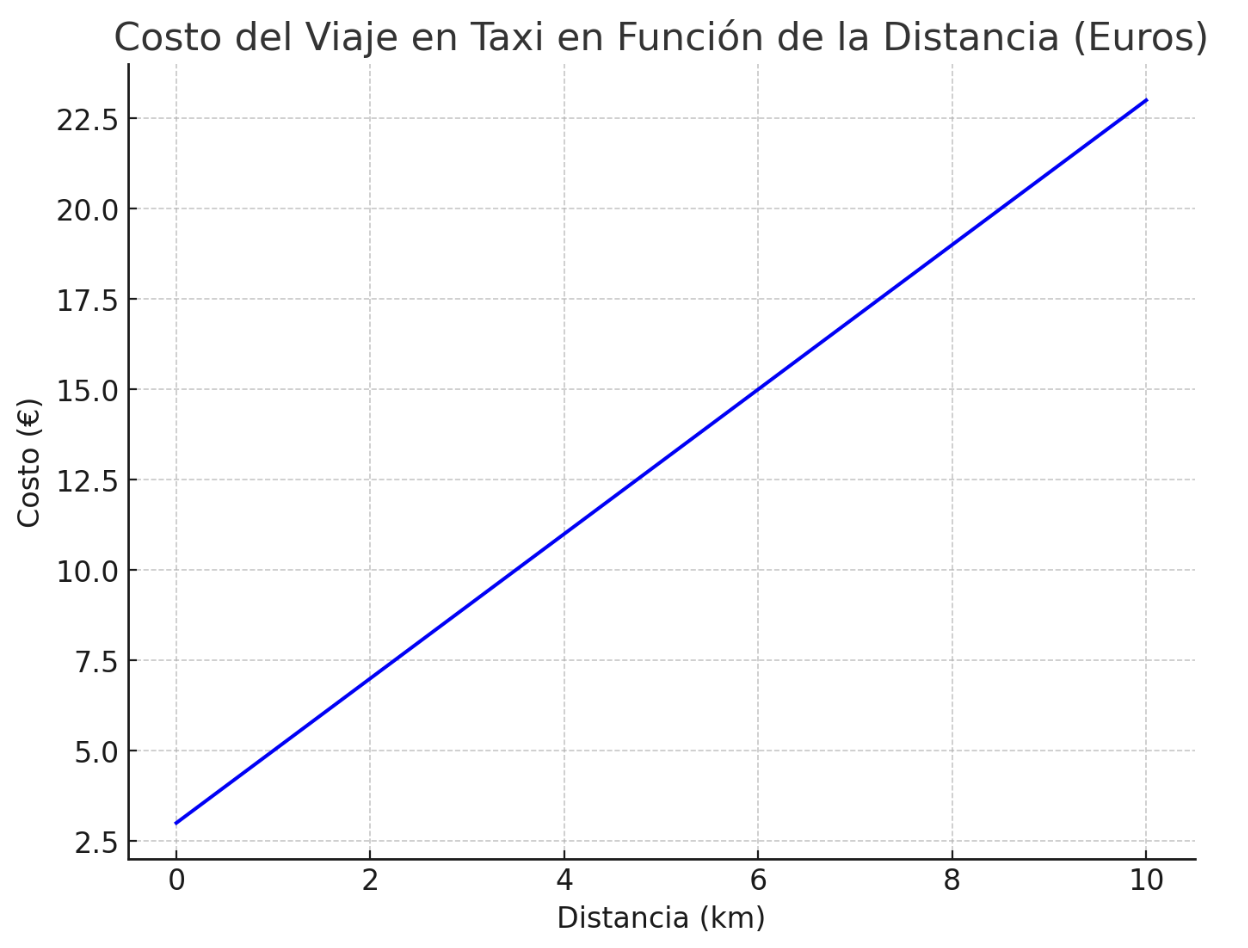
La gráfica muestra cómo el costo del viaje en taxi aumenta a medida que la distancia recorrida se incrementa. La línea recta indica una relación lineal: por cada kilómetro adicional que recorres, el costo aumenta en 2 euros, empezando desde la tarifa base de 3 euros. Este tipo de modelo es muy útil para predecir costos y planificar con anticipación en situaciones cotidianas como un viaje en taxi.

Función creciente

Una función se dice que es creciente en un intervalo $[a, b]$ si, para cualquier par de valores $x_1​$ y $x_2$​ dentro de ese intervalo donde $x_1​ < x_2$​, el valor de la función en $x_2$​ es mayor o igual que el valor de la función en $x_1$​. En otras palabras, a medida que nos movemos a lo largo del eje x dentro del intervalo de $a$ a $b$, el valor de la función nunca disminuye.

Este concepto se puede visualizar fácilmente en una gráfica. Por ejemplo, consideremos la función $f(x)=x^2$. Vamos a crear la gráfica esta función y resaltar el intervalo $[1, 2]$ para demostrar cómo la función es creciente en ese rango. En este intervalo, vemos que a medida que $x$ aumenta de $1$ a $2$, el valor de $f(x)$ también aumenta.

Función decreciente

Una función se considera decreciente en un intervalo $[a,b]$ si, para cualquier par de valores $x_1​$ y $x_2$​ dentro de ese intervalo donde $x_1​<x_2$​, el valor de la función en $x_2​$ es menor o igual que el valor de la función en $x_1$​. Esto significa que a medida que nos desplazamos a lo largo del eje x de $a$ a $b$, el valor de la función no aumenta, sino que disminuye o se mantiene constante.

Este concepto se puede visualizar fácilmente en una gráfica. Por ejemplo, consideremos la función $f(x)=-x^2$. Vamos a crear la gráfica esta función y resaltar el intervalo $[1, 2]$ para demostrar cómo la función es decreciente en ese rango. En este intervalo, vemos que a medida que $x$ aumenta de $1$ a $2$, el valor de $f(x)$ disminuye, lo que demuestra que la función es decreciente en este rango.

Un buen ejemplo de una función que es tanto creciente como decreciente en diferentes partes de su dominio es la función $f(x)= x^3-3x^2$.

Los intervalos de crecimiento están marcados en verde. En esta función, la curva es creciente en los intervalos $(−∞,0)$ y $(2,+∞)$

Matemáticamente se expresa: f(x) crece en: $(−∞,0);(2,+∞)$

Lo cual se puede observar en las partes izquierda y derecha de la gráfica respectivamente.
El intervalo de decrecimiento está marcado en púrpura. La función es decreciente en el intervalo $(0,2)$, que se encuentra en la parte central de la gráfica.

Los extremos relativos de una función son puntos en el gráfico de la función donde esta alcanza valores máximos o mínimos locales. Es importante destacar que se consideran "relativos" o "locales" porque estos puntos representan máximos o mínimos en su entorno inmediato, pero no necesariamente en todo el dominio de la función.

• Máximo Relativo (Local): Un punto en el gráfico de una función es un máximo relativo si, en un entorno pequeño alrededor de ese punto, la función no alcanza un valor mayor. Esto significa que el punto es el más alto en su área inmediata.
• Mínimo Relativo (Local): Un punto es un mínimo relativo si, en un entorno alrededor de él, la función no alcanza un valor menor. Este punto sería el más bajo en su vecindad inmediata.

Estos puntos son especialmente interesantes en el estudio de las funciones porque indican donde la función cambia su tendencia de crecimiento o decrecimiento. Para identificarlos, usualmente se utilizan técnicas de cálculo diferencial como veremos más adelante.

Veamos una gráfica donde se ilustran los extremos relativos de una función. Esto te ayudará a visualizar mejor el concepto. La función $f(x)=x^3−3x$ se muestra en azul.

• El punto en rojo marca un mínimo relativo. En este caso, el punto está en $x=1$, donde la función alcanza su valor mínimo local.
• El punto en azul señala un máximo relativo. Aquí, el punto está en $x=−1$, donde la función alcanza su valor máximo local.

Estos extremos son "relativos" o "locales" porque son máximos y mínimos en sus vecindades inmediatas, no necesariamente en todo el dominio de la función. Por ejemplo, aunque en $x=-1$ la función tiene un máximo local, existen puntos en la función donde los valores de $f(x)$ son mayores que en $x=-1$ si consideramos un rango más amplio, por ejemplo cualquier valor de x mayor que dos tiene un valor en la función más alto que el del máximo relativo considerado.

La tasa de variación media de una función en un intervalo es una medida que indica cuánto cambia el valor de la función a medida que nos movemos a lo largo de ese intervalo en el dominio de la función. En términos matemáticos, se refiere a la rapidez con la que una función cambia sus valores entre dos puntos.

Para una función $f(x)$, la tasa de variación media en un intervalo $[a,b]$ se calcula como el cambio en el valor de la función dividido por el cambio en $x$. Esto se expresa como:

\[\text{Tasa de variación media en [a, b]} = \frac{f(b) - f(a)}{b - a}\]

Esta fórmula es esencialmente la pendiente de la línea recta que conecta los puntos $(a,f(a))$ y $(b,f(b))$ en el gráfico de la función. En el contexto del cálculo, esta tasa de variación media es la base para el concepto de derivada, que es la tasa de variación instantánea de una función en un punto específico.

La tasa de variación puede ser positiva, negativa o cero:

• Positiva: Si $f(b)>f(a)$, la función está aumentando en el intervalo.
• Negativa: Si $f(b)<f(a)$, la función está disminuyendo en el intervalo.
• Cero: Si $f(b)=f(a)$, la función es constante en ese intervalo.

Este concepto es fundamental en muchas áreas de las matemáticas y sus aplicaciones, como en la física para entender la velocidad y la aceleración, en la economía para analizar tasas de cambio en variables económicas, y en la ingeniería para el diseño y análisis de sistemas y estructuras.

La siguiente gráfica muestra la función $f(x)=x^2$ con un intervalo entre los puntos $A$ y $B$. Los puntos rojos marcan los valores de la función en $x=a$ y $x=b$ ($f(a)$ y $f(b)$, respectivamente). La línea verde discontinua representa la recta secante que pasa por estos dos puntos.

En este caso concreto, los valores con los que trabajamos son los siguientes: Punto A: $(1,1)$ con lo que $a=1$ y $f(a)=1$ y Punto B: $(3,9)$ con lo que $b=3$ y $f(b)=9$.

La pendiente de esta recta secante es la tasa de variación media de la función en el intervalo $[1,3]$. Esta tasa de variación media es igual a la diferencia $f(3)−f(1)$ dividida por la diferencia $3−1$. En términos geométricos, es la pendiente de la recta que une los dos puntos en el gráfico de la función. 

\[\text{Tasa de variación media en [1, 3]} = \frac{f(3) - f(1)}{3 - 1} = \frac{9 - 1}{2} = \frac{8}{2} = 4\]