5. Una nueva magnitud: el Potencial
 Imagen en FLICKR de NASA bajo licenciaCC |
En cualquier lugar del espacio se va a sentir el efecto de la gravedad de la inmensidad de astros que pueblan el Universo ya que cada masa crea un campo gravitatorio.
Te recuerdo que definimos la intensidad de campo gravitatorio g como la fuerza gravitatoria, aquella que determinó Isaac Newton, por unidad de masa. 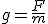
Pues bien, en este apartado vamos a ver otra magnitud que caracteriza al espacio que rodea una masa. En este caso será escalar, a diferencia del campo, que es una magnitud vectorial. Esta magnitud es el Potencial.
Para que nos resulte el estudio de esta magnitud más sencilla vamos a basarnos en lo que ya conocemos, la definición de energía potencial a partir de un trabajo:
Al igual que ![]()
Si ahora calculamos el trabajo por unidad de masa: 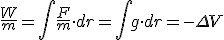
Si calculas el trabajo desarrollado por el campo gravitatorio para trasladar una masa unidad entre dos puntos el resultado final es la diferencia entre dos valores escalares, que dependerán del lugar donde estén esos puntos. A estas cifras se les conoce como potencial gravitatorio (V) en un punto creado por la masa, M, que distorsiona el espacio. Es una propiedad del espacio y es independiente de la masa m colocada en un punto cualquiera.
Una cuestión importante, tal y como vimos en el apartado de energía potencial, es establecer un punto de referencia. El elegido es el infinito. En tal posición se va a asignar el valor para el potencial de cero 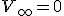 .
.
Así podemos definir el potencial gravitatorio como el trabajo que realiza el campo para trasladar la unidad de masa de dicho punto al infinito.
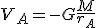
Su unidad en el Sistema Internacional es J/kg.
Importante
Debes tener clara la siguiente idea: el campo gravitatorio (g) y el potencial gravitatorio (V) miden básicamente lo mismo: las propiedades del espacio que rodea a una masa, g lo hace de forma vectorial y V de forma escalar.
Por otro lado, si comparamos el valor de la energía potencial en el punto A con el valor del potencial en ese punto podemos observar que se cumple que:
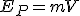
el potencial gravitatorio creado por la masa M en un punto se define como la energía que adquiriría un cuerpo de masa unidad colocado en ese punto.
Como ya vimos, el trabajo para trasladar un cuerpo de un lugar a otro es la diferencia de las energías potenciales que tiene el cuerpo en esos dos puntos, podemos determinar entonces que la variación del potencial es el trabajo que realiza el campo para trasladar una masa de 1 kg desde A hasta B.
Para saber más
 |
| Imagen de elaboración propia |
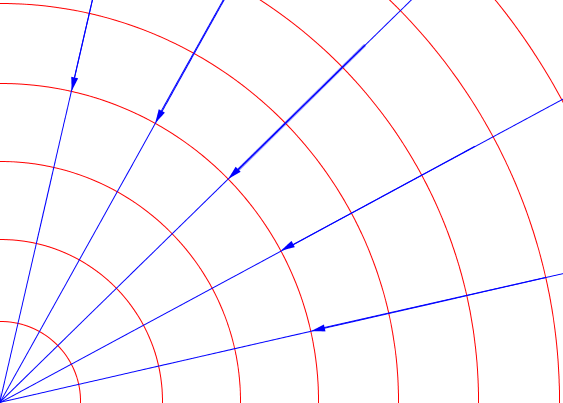
Si se pudieran unir todos los puntos que tienen el mismo potencial se tendría una superficie, son las llamadas SUPERFICIES EQUIPOTENCIALES.
Estas superficies tienen tres características importantes que debes conocer ya que las mismas te posibilitarán interpretar la situación y realizar cálculos oportunos y rápidos.
- Por cada punto sólo puede pasar una única superficie equipotencial.
- El trabajo que se requiere para trasladar un cuerpo de un punto a otro de la misma superficie equipotencial es nulo.
- Los vectores intensidad de campo son perpendiculares a tales superficies equipotenciales y, por tanto, las líneas de campo son normales a las mismas.
¿Cómo son las superficies equipotenciales en el caso del potencial gravitatorio?Imagina que un satélite gira en torno a un planeta. El satélite se mueve pero siempre estará a la misma distancia. ¿Cómo varía el potencial del satélite debido a este movimiento? si analizas la expresión del potencial verás que el valor de este sólo depende de la masa del planeta y de la distancia a este. En el caso en que nos hayamos no varían ni lo uno ni lo otro, así que el potencial es constante.
Por ello, en el caso del campo gravitatorio, las superficies equipotenciales tendrán la forma de esferas concéntricas centradas en la masa que crea el campo, tal y como puedes ver en la imagen.
Caso práctico
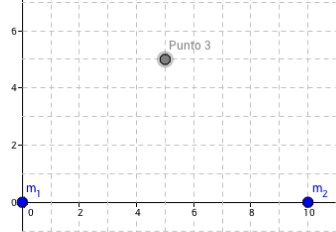
En la animación puedes colocar las masas en diferentes puntos y variar su magnitud así como el punto 3. Haciendo clic puedes mostrar los puntos sobre el plano, visualizar solo la solución del problema o todo el desarrollo matemático. Te recomendamos que estudies un caso y que luego practiques cambiando de posición las masas y sus valores.
Caso práctico
 |
| Imagen de elaboración propia |
Usa la animación anterior para calcular los valores del potencial gravitatorio.
Reflexión
El potencial gravitatorio ¿aumenta o disminuye si nos alejamos de la masa que genera un campo a su alrededor?