4. Principio de conservación de la Energía Mecánica

Una vez llegados a este punto podemos hacer un análisis de la energía total de un sistema, recuerda, la llamada energía mecánica: es la suma de la energía cinética y las energías potenciales que tiene una partícula.

$E_{M}= E_{C}+E_{P}$

Aplicando lo que hemos conocido en este tema, el teorema de las fuerzas vivas: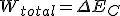

y el teorema de la energía potencial: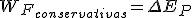

y considerando la situación en que sólo actúen fuerzas conservativas nos queda que:

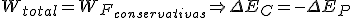
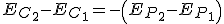y quitando paréntesis:

Si redistribuimos los términos obtenemos una expresión muy importante en física que se conoce como principio de conservación de la energía mecánica:

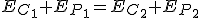
Se puede enunciar del siguiente modo:

Si sobre un cuerpo sólo actúan fuerzas conservativas, su energía mecánica se mantiene constante en todo momento, es decir, se conserva.

En muchos problemas, si se traslada un cuerpo entre dos puntos debido a la acción de una fuerza gravitatoria (y no hay fuerzas no conservativas) entonces podremos aplicar este principio.

Para saber más

Si además de las fuerzas conservativas actúan otras fuerzas que no son conservativas, por ejemplo, la fuerza de rozamiento:

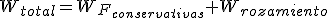
Obtenemos lo siguiente:

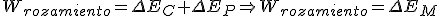
Si en un determinado sistema actúan tanto fuerzas conservativas como no conservativas, se verifica que la variación de la energía mecánica entre la situación inicial y final coincide en valor con trabajo realizado por las fuerzas no conservativas. Dicho de otra forma, la energía mecánica de un cuerpo sólo es modificada si actúan sobre él fuerzas no conservativas.

Animación de Magnus Colossus disponible bajo la licencia CC-BY-SA vía Wikimedia Commons.

En el ejemplo que se ilustra, una montaña rusa, la energía mecánica no se mantiene constante ya que hay una pérdida de energía debida al rozamiento de los vagones con las vías.