3.1.1 Energía potencial gravitatoria
 |
| Imagen de Agusx1211 en Wikimedia Commons bajoCC-BY-SA-4.0 |
En el primer tema de la unidad estudiaste la fuerza gravitatoria, que es aquella interacción entre dos cuerpos separados una cierta distancia.
Pues bien, esta fuerza gravitatoria es conservativa, esto nos permite hacer un estudio de la energía potencial y sus variaciones en el caso de los planetas en el Universo, vamos a trabajar la función energía potencial gravitatoria.
Un cuerpo tendrá energía potencial gravitatoria cuando actúe sobre él una fuerza gravitatoria y su valor dependerá de la posición en la que se encuentre dicho cuerpo. Aplicando la definición de fuerza gravitatoria
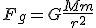
obtenemos que el trabajo desarrollado valdrá:
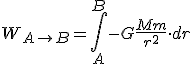
Para resolver esta integral lo primero que hemos hecho es "sacar de ella" las constantes, quedando así una integral inmediata que se resuelve fácilmente.
Debes saber que ![]() por tanto:
por tanto:
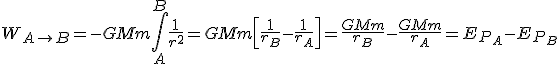
(si quieres saber algo más sobre las integrales inmediatas puedes ver este vídeo)
Ya ves que calculando el trabajo realizado por la fuerza gravitatoria al trasladar un cuerpo desde un punto a otro sólo se puede calcular la variación en la energía potencial que sufre ese cuerpo, pero no tenemos datos suficientes para saber el valor de la energía potencial gravitatoria en cada punto. Recuerda, hay que tomar una referencia.
Por convenio, cuando se trata de cuerpos en el espacio se suele utilizar como referencia cero la energía potencial en el infinito (cuando los cuerpos están muy alejados) 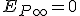
![]()
Según lo anterior la energía potencial gravitatoria se puede definir como:
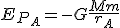
Es la energía necesaria que hay que suministrar al cuerpo m para vencer la fuerza gravitatoria y trasladar el cuerpo desde el punto A hasta el infinito
La expresión de la energía potencial es negativa porque, según nuestra referencia escogida, queremos llevar el cuerpo al infinito y como la fuerza gravitatoria es siempre atractiva trasladamos el cuerpo en contra de la fuerza gravitatoria, por tanto debemos suministrar una energía para vencer esa fuerza y mover el cuerpo.
Importante
 |
| Imagen de creación propia |
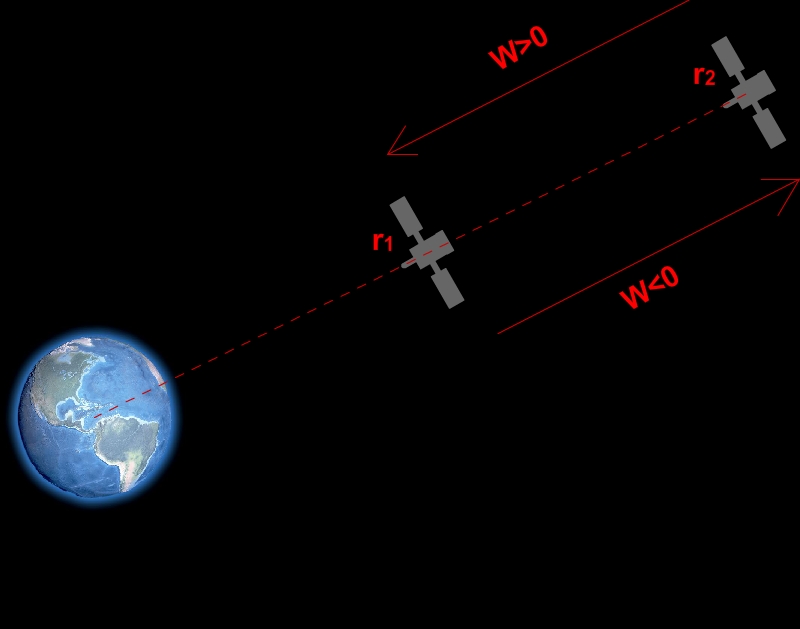
Observa la imagen. En ella se ve representado un satélite en dos posiciones distintas, a una distancia r1 de la Tierra, y a una distancia mayor, r2.
Analicemos las dos posibles situaciones en las que el satélite se mueve respecto del planeta Tierra, acercándose o alejándose de esta.
• Si el satélite se acerca, pasando de la posición r2 a r1el trabajo realizado es positivo (se mueve a favor del campo, que es atractivo), por tanto disminuye la energía potencial del satélite.
• Si por el contrario el satélite se alejara el trabajo sería negativo aumentando entonces la energía potencial de este.
Para saber más
Para cada tipo de fuerza conservativa que existe puede definirse una energía potencial.
La fuerza gravitatoria es conservativa por tanto se puede definir una energía potencial gravitatoria.
![]()
Otro ejemplo es la fuerza elástica (aquella que hace que un muelle vuelva a su posición de equilibrio toda vez que se suelta al haber sido estirado o comprimido). Por tanto puede hablarse de una energía potencial elástica.
![]()
Una tercera fuerza conservativa que permite definir una energía potencial es la fuerza electrostática, que será objeto de estudio en la unidad siguiente.
Caso práctico
Un punto A está situado a 500 km sobre la superficie de la Tierra y un punto B en la misma superficie. Calcula el trabajo realizado por el campo cuando un satélite de 5000 kg se traslada desde A hasta B.
Datos: Masa de la Tierra: 6·1024 kg; radio de la Tierra: 6400 km; constante de gravitación universal: G = 6,67·10-11 N·m2/kg2
Caso práctico
En la animación puedes colocar las masas en diferentes puntos y variar su magnitud. Haciendo clic puedes mostrar los puntos sobre el plano, visualizar la solución del problema o todo el desarrollo matemático. Te recomendamos que estudies un caso y que luego practiques cambiando de posición las masas y sus valores.