1. Secuenciación del reto
Tras haber completado la situación de aprendizaje, es el momento de embarcarte en una aplicación práctica y sumamente relevante de las nuevas habilidades que has adquirido. Este paso representa una oportunidad excepcional para transformar los conceptos teóricos en una realidad tangible, lo que te permitirá consolidar y expandir tu comprensión.
Ahora te enfrentas a un desafío que no solo pone a prueba tu habilidad para aplicar el cálculo diferencial y la optimización, sino que también te brinda la oportunidad de contribuir significativamente al desarrollo sostenible de Andalucía, una región famosa por su abundante y exquisita producción de tomates.
Te presentamos el siguiente reto: optimizar el diseño de una lata de tomate con forma cilíndrica, utilizando la menor cantidad de latón posible. Este ejercicio no es solo una cuestión de minimizar costos, sino una misión para reducir el impacto ambiental asociado con el envasado de uno de los productos más emblemáticos de Andalucía. A través del uso de derivadas, identificarás los valores que minimizan el uso de materiales sin comprometer la funcionalidad y la integridad del envase.
Este desafío te permite no solo aplicar las herramientas matemáticas de cálculo diferencial y optimización de manera práctica, sino también situarte en el centro de un escenario real, donde tus decisiones de diseño pueden influir positivamente en la sostenibilidad y la economía de la región.
Te animo a abordar este proyecto con creatividad e innovación, siempre manteniendo un firme compromiso hacia la sostenibilidad. Recuerda que, al buscar soluciones eficientes y creativas, no solo estás demostrando tu competencia matemática, sino también contribuyendo activamente a la construcción de un futuro más verde y próspero.
¡Adelante, que tu ingenio y habilidades te guíen hacia un diseño óptimo y sostenible!
Redactar un documento (Portafolio) que contenga los siguientes apartados, asegurándote de resolver todas las actividades que se proponen.
1. Portada
Datos de la portada
- Título del Portafolio
- Nombre del autor
- Fecha de elaboración
- Imagen ilustrativa relacionada con el tema
Ayuda:
Adobe Express es una herramienta online gratuita para fotografía y diseño que te permite crear proyectos que destaquen gracias a la inteligencia artificial generativa de Adobe Firefly. Puedes editar imágenes, vídeos y PDF en unos pocos clics, usando plantillas profesionales, efectos de texto, relleno generativo y mucho más. Aquí dispones también de un manual online para tus consultas.
2. Matemáticos pioneros del cálculo diferencial
Actividad 1.
Investiga la vida y obra de Isaac Newton y de Gottfried Wilhelm Leibniz y luego responde a las siguientes cuestiones:
- Realiza un breve resumen biográfico de cada matemático.
- Resume las principales contribuciones y logros al desarrollo del cálculo diferencial de cada uno de ellos.
- Redacta un texto argumentativo expresando tu opinión acerca de quién realizó la contribución más significativa.
Ayuda:
- Isaac Newton en Wikipedia
- Gottfried Leibniz en Wikipedia
- Blog sobre los creadores del cálculo diferencial
- Vídeo sobre el descubrimiento del cálculo
3. Modelizamos y optimizamos
Actividad 2.
En la siguiente tabla se muestra un resumen de la producción anual de tomate en España, en millones de kilogramos (KG), desde 2007 hasta 2021 (fuentes 1, 2):
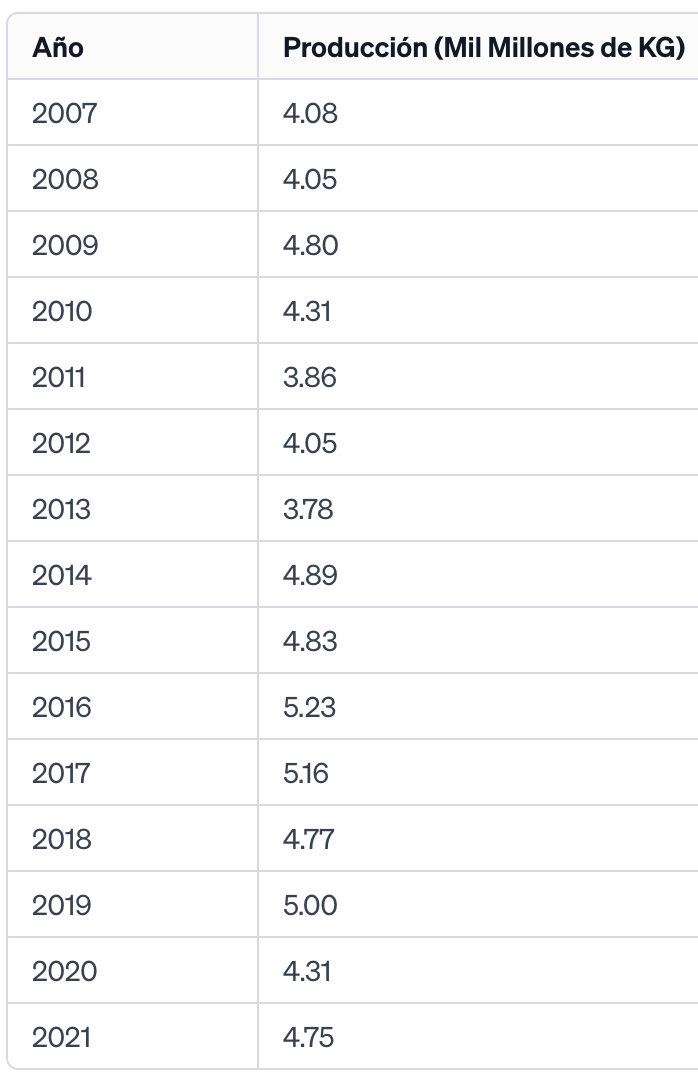
a. Compara la tasa de variación media de la producción de tomate en España entre 2007-2009 y 2019-2021. ¿En cuál de estos periodos la producción de tomate tuvo una mayor tasa de crecimiento?
En la siguiente gráfica se muestra la producción de tomate en España desde 2007 hasta 2021.
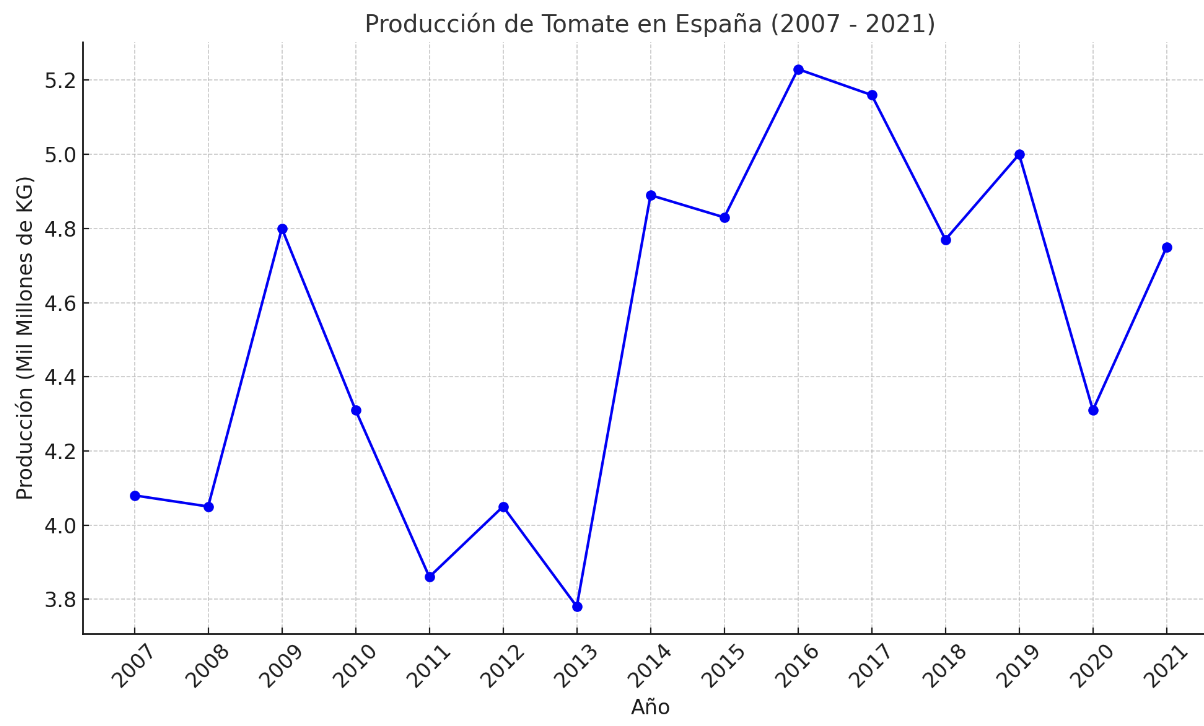
b. Encuentra el intervalo de años en el que la tasa de crecimiento de la producción de tomate fue máxima, interpretando esto como la pendiente máxima en un segmento de la función.
c. Si el impacto ambiental en la producción de tomate se considera proporcional a la cantidad producida, identifica el año en el que este impacto fue máximo.
Actividad 3.

La función de beneficios de una empresa de tomate envasado, en miles de euros, en función de la cantidad de tomates procesados, se modela con un polinomio de grado 3: $B(x)=−0.1x^3+2x^2+x$, donde $x$ representa las toneladas de tomates procesados.
- ¿Cuál es la cantidad óptima de toneladas de tomates que la empresa debe procesar para alcanzar el máximo beneficio posible?
- Al procesar esta cantidad óptima de tomates, ¿cuál es el beneficio máximo que la empresa puede esperar obtener?
Actividad 4.

Se ha desarrollado un modelo para entender cómo los residuos generados en la producción de tomate envasado varían en función de la cantidad de tomate procesado. La cantidad de residuos, en toneladas, se representa mediante la función $ W(x) = 725 + 3x^2 $, donde \( x \) es la cantidad de tomates procesados, también en toneladas.
Por otro lado, los costos asociados con la gestión de estos residuos se modelan con la función \( M(x) = 2x-13 \), que es proporcional a la cantidad de producción.
Para promover prácticas más sostenibles, la empresa está interesada en minimizar la relación entre la cantidad de residuos generados y los costos de gestión. Esta relación se describe con la función $ D(x) = {\large{\frac{W(x)}{M(x)}}} $.
- ¿Cuál es la cantidad óptima de tomates procesados (en toneladas) para minimizar la función \( D(x)\)?
- ¿Cuál es el valor mínimo de la función \( D(x)\) cuando se procesa esta cantidad óptima de tomates?
4. Resolvemos el reto
Actividad 5.
Una empresa de alimentos desea diseñar una lata de tomate cilíndrica con tapa, con un volumen de 500 ml (mililitros), utilizando la menor cantidad posible de latón. El objetivo es determinar las dimensiones óptimas de la lata (radio y altura) para minimizar la superficie total del material utilizado, garantizando al mismo tiempo que la lata tenga el volumen requerido.
Datos y Restricciones:
El volumen de la lata debe ser exactamente 500 ml.
La lata tiene una base y una tapa circulares, y ambas tienen el mismo radio.
La lata debe ser un cilindro recto.
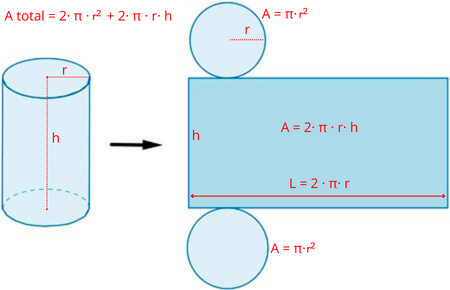
Formulación Matemática:
- Sea \( r \) el radio de la base y la tapa de la lata, y \( h \) la altura del cilindro.
- La superficie total \( A \) de la lata, que incluye las áreas de la base, la tapa y la superficie lateral, se calcula como: \[ A = 2\pi r^2 + 2\pi rh \]
- El volumen \( V \) del cilindro se da por: \[ V = \pi r^2 h \]
- Dado que el volumen debe ser 500 ml, tenemos la restricción: \[ \pi r^2 h = 500 \]
- El objetivo es minimizar \( A \) sujeto a la restricción de que \( V = 500 \) ml.
Pregunta:
¿Cuáles deben ser los valores de \(r\) y \(h\) para minimizar la superficie total de la lata de tomate, asegurando que su volumen sea de 500 ml?