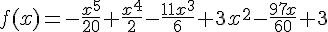2.2. Definición de punto de inflexión

Autobus

Ahora queremos que te pongas en una situación concreta. Piensa que vas en un autobús urbano de una gran ciudad. Vas de pie agarrado a la barra de sujeción y, de pronto, el autobús comienza a girar en una esquina. ¿No te ha ocurrido alguna vez que de pronto tu cuerpo parece que se inclina hacia un lado y en un preciso momento cambia y ahora parece que se inclina para el lado contrario? Si has tenido alguna vez esa sensación enhorabuena, acabas de pasar por un punto de inflexión.

Importante

Punto de inflexión

Un punto de inflexión es aquel en el que la función cambia de curvatura, es decir, en el que pasa de cóncava a convexa o viceversa.

 

Si trazamos una tangente a la función en ese punto se puede apreciar que a un lado del punto la función queda por encima de la recta tangente y al otro lado por debajo.

Como en el punto de inflexión la función pasa de cóncava () a convexa (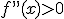), lo normal es que en ese punto la función se anule. Compruebalo en la siguiente ventana observando que pasa en los puntos x=-3, x=0 y x=2, que son puntos de inflexión de la función.

Applet alojado en GeoGebra. Licencia CC

Importante

Si una función f cumple en un valor x=a que 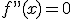y 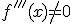entonces la función tiene en el punto de valor x=a un punto de inflexión.

 

Si es complicado el cálculo de la derivada tercera, lo usual es estudiar el signo de la segunda derivada antes y después del punto x=a. Si cambia su signo entonces es punto de inflexión.

Ejemplo o ejercicio resuelto

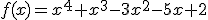
Determina los puntos de inflexión de la función

AV - Actividad de Espacios en Blanco

Mandos compañía petrolera
Foto tomada del Banco de Imágenes del ITE.

En una compañía petrolifera están estudiando el número de miles de bidones de combustible que han servido en las cuatro primeras semanas del mes. Les interesa conocer si el aumento o disminución ha sido muy rápido o no y para ello quieren localizar los puntos de inflexión en ese reparto.

Después del estudio realizado han aproximado la entrega de combustible a la función siguiente:

Los puntos de inflexión de esa función se obtienen en:

(1, )

,

( , )

Enable JavaScript

En todas las actividades que hemos realizado en el tema siempre nos han dado una función y hemos estudiado su monotonía y su curvatura. Pero a veces nos piden encontrar una función de la que conocemos algunas características. Observa el siguiente ejercicio resuelto.

Ejemplo o ejercicio resuelto

Encuentra una función polinómica de tercer grado sabiendo que tiene un punto de inflexión en el punto (1,-3) y alcanza un extremo local en el (-1,13).
En el apartado siguiente, que incluye ejercicios que han aparecido en las Pruebas de Acceso a la Universidad, puedes encontrar más ejemplos de cálculo de monotonía y curvatura de una función y de ejercicios como este último.