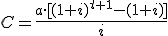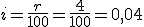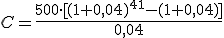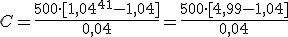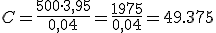3.2. Cálculo del capital final
Por ejemplo: una persona puede hacer una cuenta vivienda, y entrega cada mes una cantidad de dinero y cuando pasen los años establecidos tendrá en su cuenta el dinero que ha ido entregando más los intereses que dicho dinero ha producido.
Cuando el periodo de entrega de dinero a la operación de capitalización es anual se habla de anualidad de capitalización.
Caso práctico
Anualidades de capitalización
En primer lugar, nos planteamos la idea de crear un fondo de capitalización. Para eso cada determinado período de tiempo, en este caso, cada año entregaremos una cierta cantidad de dinero durante varios años. Así, pensemos que vamos a aportar a euros, durante t años, a un interés compuesto del r % anual. ¿Cuánto dinero tendremos al final de los t años?
Vamos a plantearlo con un ejemplo: Jorge, con 60 años, abre en un banco un plan de pensiones. Al comienzo de cada año y hasta la edad de su jubilación, a los 65 años, aportará 1.000 €, siendo el interés del 6 % anual.
¿Qué capital habrá acumulado cuando se jubile?
|
PRINCIPIO DEL: |
APORTA: | FINAL DEL: | CAPITAL ACUMULADO: |
|---|---|---|---|
|
Primer año (60 AÑOS) |
1.000 € |
Primer año |
|
| Observa que al capital aportado hemos sumado los intereses generados por ese dinero durante el año. Es muy importante que te fijes en que la operación se resume en multiplicar el dinero que tenemos al principio del período (en este caso los 1.000 € aportados) por 1,06 (es decir, 1 más el resultado de dividir el interés anual entre 100). | |||
|
Segundo año (61 AÑOS) |
1.000 € |
Segundo año |
|
| De nuevo hemos multiplicado la cantidad acumulada al principio del período (los 1.060 € ahorrados más los 1.000 € de la nueva aportación) por 1,06. | |||
|
Tercer año (62 AÑOS) |
1.000 € |
Tercer año |
|
|
Cuarto año (63 AÑOS) |
1.000 € |
Cuarto año |
|
|
Quinto año (64 AÑOS) |
1.000 € |
Quinto año (Final de la operación) |
|
| Por tanto, al finalizar la operación se encuentra con 5.975,33 €. Es fundamental que observes que en cada paso hemos multiplicado el capital acumulado por 1,06 (1+0,06). | |||
Comprueba lo aprendido
En el punto anterior hemos obtenido el dinero que habría acumulado Jorge, pero haciendo el proceso completo, año a año. Si fuesen muchos años esto nos complicaría bastante el proceso, ¿no?
Reflexionemos sobre otro ejemplo:
Caso práctico
El hijo de Jorge, viendo que su padre ha conseguido un capital final bastante pequeño en el momento de jubilación, decide hacerse un plan de pensiones desde joven. Ahora tiene 25 años y se plantea aportar 500 € cada año, hasta su jubilación (a los 65 años), en una entidad financiera, en la que le ofrecen un 4 % de interés anual.
En la siguiente tabla, iremos desarrollando la situación planteada, pero a la vez, intentaremos sacar conclusiones que nos puedan servir para cualquier caso. Se trata de encontrar un modelo que nos permita encontrar el capital que obtendremos al final sin hacer el recorrido por todos los años que dure la operación de capitalización. Este modelo sería: Se aportan a euros, durante t años, a un interés compuesto del r % anual.
¿Cuánto dinero tendremos al final de esos t años?
| AÑO | EJEMPLO | GENERALIZACIÓN |
|
Primer año |
Aporta 500 € y a final de año tiene:
|
Aporta a € y a final de año tiene:
|
Recuerda que para obtener el capital acumulado a final de un período basta con multiplicar el dinero disponible al principio del mismo por 1 más el interés en tanto por uno (es decir, el interés dividido por 100). Aquí, hemos llamado i al resultado de 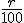 . . |
||
|
Segundo año |
Aporta 500 € y a final de año tiene:
|
Aporta a € y a final de año tiene:
|
|
Tercer año |
Aporta 500 € y a final de año tiene:
|
Aporta a € y a final de año tiene:
|
|
Insistimos en hacer notar que siempre, en cada paso, al capital acumulado le sumamos la aportación periódica y multiplicamos por 1+i. Observa la expresión teórica que da el capital en cada paso (fíjate en los sumandos que tiene, tantos como el número del período, y en los exponentes de (1+i)). Claro, seguir con este proceso hasta el final de esta operación (que durará 40 años) sería demasiado laborioso y pesado. Convendría tener una expresión para obtener el resultado sin hacer el cálculo todos los años. |
||
| Tras 40 años | ¿Qué capital tendrá este joven pasados los 40 años?. Vamos a intentar razonarlo sobre nuestro desarrollo teórico. | |
| TRAS t AÑOS |
Sabemos que el capital acumulado será la suma de lo aportado más los intereses generados. Si nos fijamos en lo que ha ocurrido en los 3 primeros años, la fórmula para el capital acumulado al cabo de t años sería:
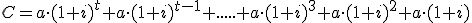
Como comentábamos antes, ha de tener t sumandos ya que hablamos de t años (todos los sumandos con el factor común a), y el primer sumando lleva el factor (1+i) elevado al número de años (t), el segundo a t-1, y así, bajando de exponente hasta quedarse en 1+i. Sin embargo, pensarás que si no se lo que hay en los puntos suspensivos cómo voy a sumar. No te preocupes, en realidad utilizando propiedades de las progresiones geométricas (que no necesitas conocer, pero que podrás estudiar si lo deseas en este enlace) se llega a la siguiente fórmula, que nos permite hacer el cálculo deseado:
|
|
Apliquemos la fórmula al plan de pensiones del hijo de Jorge:
| APORTACIÓN PERIÓDICA: | INTERÉS ANUAL: | TIEMPO: |
| a = 500 € |
r = 4%
|
t = 40 años |
|
|
||
Importante
Por lo tanto, para calcular el capital final después de t años de ahorro con un interés i, utilizamos la fórmula:
![]()
Donde a es la anualidad.
Caso práctico
Recordemos la operación de capitalización realizada por Jorge. Con 60 años abrió en un banco un plan de pensiones. Al comienzo de cada año y hasta la edad de su jubilación, a los 65 años, aportará 1.000 €, siendo el interés del 6 % anual.
¿Qué capital habrá acumulado cuando se jubile?
Intenta resolver este problema utilizando la fórmula, no dando todos los pasos como en el apartado anterior.
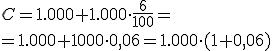
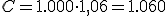 €.
€.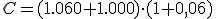
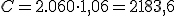 €
€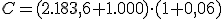
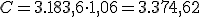 €
€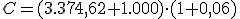
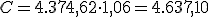 €
€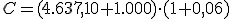
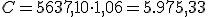 €
€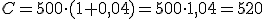 €
€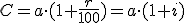 €
€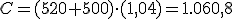
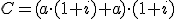
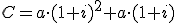 €
€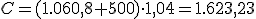 €
€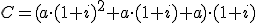
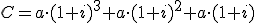 €
€