2.2 Cálculo de las cuotas
Cuotas mensuales
En el apartado anterior te habrás quedado pensando ¿cómo se calculan los 847, que dice el banco que voy a pagar?
En este apartado vamos a razonarlo y lo vas a entender.

Imagen de 22594 en Pixabay. Licencia CC
Tomemos los datos utilizamos anteriormente:
Capital concedido (C): 18.000 €
Tanto por ciento (r): 12 %
Tiempo (t): 2 años
Mensualidad: (m) : ?
Lo que vas a ver a continuación es lo que produce una mensualidad m al 1% mensual durante el tiempo que lo tiene el banco, desde 0 a 23.
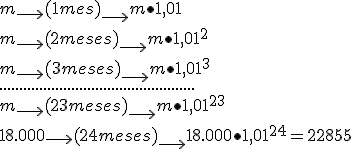
Sumando nos sale:
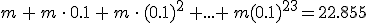
y despejando queda:

Importante
Fórmula de mensualidad para amortizar un préstamo
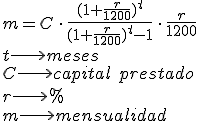
Reflexiona
 |
Imagina el siguiente cálculo:
18.000 · 0,12=2.160 € al año (ha aplicado el 12% a la cantidad pedida).
Como son dos años, pensó, serán 4.320. Al banco debo pagar 18.000+4.320= 22.320 en 24 meses. Dividiendo 22.320 entre 24 se obtiene una cuota mensual de 930 €.
¿Por qué no coinciden?
Cuotas anuales
Por supuesto que existen créditos cuya amortización se hace año a año. Como en el apartado anterior vamos a suponer que los 18.000 € que hemos pedido lo pagamos en dos años, pero con la amortización anual.
Para que te hagas una idea, si el préstamo se nos hace efectivo el 1 de diciembre de 2010 la 1ª anualidad se paga el 30 de noviembre de 2011 y la segunda el mismo día de 2012.
Capital concedido (C): 18.000 €
Tanto por ciento (r): 12 %
Tiempo (t): 2 años
Anualidad (a) : ?
Importante
La anualidad de un préstamo se calcula a través de la siguiente fórmula:
![]()
Sólo se diferencia en que, r (tanto por ciento) se divide por 1200, si es mes a mes o por 100, si es año a año.
Eso sí ¡CUIDADO! t, en este caso, son AÑOS
Caso práctico
Calculemos la anualidad de este préstamo.
Si saldamos la deuda de 18.000 con dos pagos de 10.650,56 € son 21.301,12 €, lo que supone que hemos pagado al banco 3.301,12 € de intereses.
¿Recuerdas qué intereses se pagó saldando el préstamo con mensualidades? Te lo recuerdo:
24 mensualidades de 847 € ello supone (multiplicando por 24)=20.328 €, y por tanto (le quitamos 18.000): 2.328 €.
¿Por qué esa diferencia?