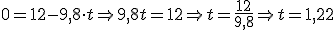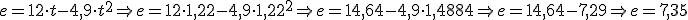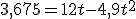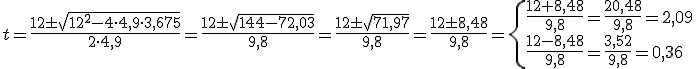Aplicamos las ecuaciones del MRUA
Actividad de Lectura

Imagen: flickr.com / Ventura2
¡Vamos, vamos… qué hay prisa!
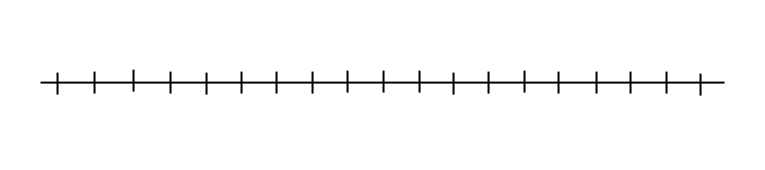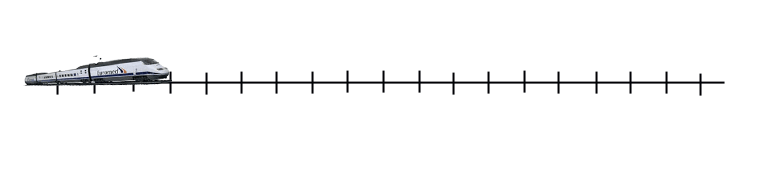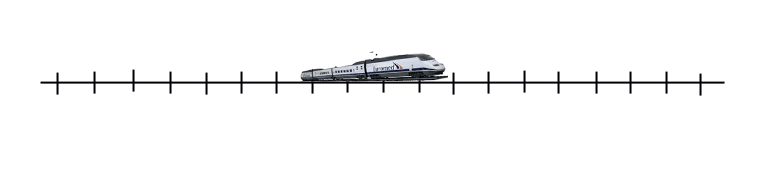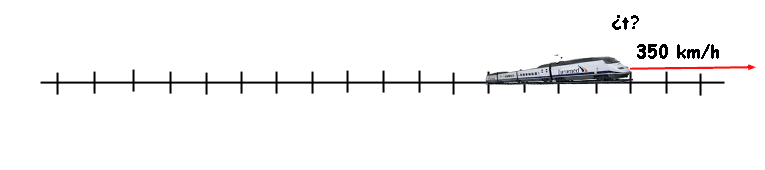
El AVE S-103 que une Madrid y Barcelona puede alcanzar una velocidad maxima de hasta 350 km/h. Claro, que ir tan rápido no se consigue así como así... y es que el bicho tiene una masa de "solo" 425.000 kg, que no son fáciles de acelerar (como verás en el tema 4 de este mismo bloque)
De hecho, pasa de cero a cien en unos 50 s...
- ¿Con qué aceleración arranca el AVE S-103?
- Si mantuviera esa aceleración constante, ¿cuánto tiempo tardaría en alcanzar su velocidad máxima?
Pre-conocimiento
Parece más fácil… pero es lo mismo
En algunas situaciones, como la del problema que acabas de estudiar, en el que conocíamos las velocidades inicial y final de un MRUA y el tiempo y queríamos averiguar la aceleración que ha tenido el movimiento, parece más fácil aplicar la propia definición de la aceleración:
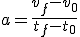
Pero... en el fondo... es lo mismo que has estudiado en el ejemplo...
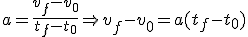
y si, como en este caso, tanto v0 como t0 valen cero... nos queda 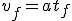 , que es la misma ecuación que hemos aplicado arriba.
, que es la misma ecuación que hemos aplicado arriba.
Actividad de Lectura

Imagen: © Aleksandr Ugorenkov | Dreamstime.com
¡Echa el freno… !
Pero si difícil es poner al tren a esas velocidades... ¡No veas lo que cuesta pararlo!
La aceleración con la que puede frenar el S-103 es, tan solo, de 1,21 m/s2 (es muy difícil detener un vehículo tan pesado).
¿Cuánto tiempo tardará en detenerse el tren si frena de manera constante y empieza a frenar cuando va a su máxima velocidad?
Mientras frena... avanza, por supuesto. Pero ¿qué distancia recorrerá desde que empieza la frenada hasta que, por fin, consigue detenerse?
Hay un MRUA que es especialmente importante por "lo cerca" que lo tenemos.
Al decir "cerca" nos referimos a que es un fenómeno muy cotidiano; todos los días vemos ejemplos de ese movimiento (más o menos) ¿O acaso no has visto nunca algo que se cae desde cierta altura, como una hoja que cae de un árbol, por ejemplo? ¿O no has lanzado algo verticalmente hacia arriba (una piedra, una pelota,...)
Pues bien, el movimiento de esos objetos que caen o que se lanzan verticalmente hacia arriba es un MRUA, cuya aceleración constante vale 9,8 m/s2 y SIEMPRE está dirigida hacia el centro de la Tierra.
A esa aceleración con la que caen los objetos se la suele llamar la aceleración de la gravedad y se la suele representar por la letra g.
El estudio de estos movimientos es muy sencillo porque... ¡Siempre sabemos lo que vale la aceleración!
Actividad de Lectura

Imagen: dreamstime
Todo empezó con una manzana… en caída libre
Según cuenta la leyenda, Newton llevaba ya bastante tiempo dándole vueltas al tema de porqué caían los cuerpos, hasta que un día... se le cayó la manzana en la cabeza.
Sí, así como lo lees. Estaba leyendo bajo un gran manzano cuando una manzana madura se desprendió del árbol y fue a caer justo a su lado. Como te digo, la leyenda cuenta que entonces Newton comprendió por fin porqué las cosas caían como caían.
Pero claro... eso es... solo una leyenda.
Imagina que Newton hubiese "acechado" otra manzana (no dudes que si la leyenda es cierta, seguro que lo hizo) y hubiese medido el tiempo que tardase en caer: 85 centésimas de segundo, es decir, 0,85 s.
¿Podría haber podido calcular Newton con esos datos desde qué altura cayó la manzana? ¿Y tú, lo podrías calcular?

Imagen: sxc.hu
¿Y si en lugar de una deliciosa manzana, hubiera sido una hoja la que se cae del árbol, pero desde la misma altura?
¿Habría tardado el mismo tiempo? ¿Tal vez más...?
Tu experiencia te dice que... ¡POR SUPUESTO QUE SÍ! La hoja tardaría más tiempo en caer ¿Verdad?
Pero... ¿Y si no hubiera aire? ¿Qué pasaría si tanto la manzana como la hoja cayesen... pero en el vacío, donde no la pudiera frenar el aire?
Pre-conocimiento
Parece mentira pero…
... en ausencia de aire, en el vacío, todos los cuerpos caen de la misma forma, con la misma aceleración, con la misma velocidad. Es algo que no nos imaginamos porque, claro, siempre hemos visto las cosas caer "habiendo aire".
Es algo que ya nos dejó dicho Galileo hace muchos, muchos años (en el siglo XVII), y que los astronautas que llegaron a la Luna en la misión Apolo XV pudieron comprobar "en directo" (allí no hay aire que frene la caída de los cuerpos y, además, la aceleración de la gravedad es mucho más pequeña que en la Tierra, solo 1,6 m/s2, con lo que "se ve mejor", las cosas caen más despacio)
Transcripción del Diario de a bordo
167:22:06 Scott: Bien, en mi mano izquierda tengo una pluma y en la derecha un martillo. Y supongo que una de las razones por la que estamos hoy aquí es por un caballero llamado Galileo, porque hace mucho tiempo hizo un importante descubrimiento sobre los cuerpos que caen en un campo gravitatorio. Y pensamos que la Luna sería el mejor lugar para confirmar sus ideas.
167:22:28 Scott: Ahora lo intentaremos para que lo veas. Concretamente, la pluma es de un halcón, una pluma de halcón de nuestro Halcón (se refiere al halcón del escudo de..). Ahora soltaremos los dos a la vez y, esperemos, llegarán al suelo a la vez. (Pausa)
167:22:43 Scott: ¡qué te parece!
167:22:45 Allen: ¡qué te parece! (Aplausos en Houston)167:22:46 Scott: Lo que demuestra que las ideas de Galileo eran correctas. (Pausa)
Actividad de Lectura
|
|
Caída libre pero… hacia arriba
Se suele decir que "todo lo que sube baja" y, al menos en lo que se refiere al movimiento de caída libre podríamos añadir... "y baja lo mismo que ha subido, pero al revés". Con este ejemplo seguro que lo entiendes.
Cuando se lanza un cuerpo hacia arriba verticalmente, como su velocidad va hacia arriba, pero su aceleración (la de la gravedad) va hacia abajo, el cuerpo va frenando, frenando, frenando... hasta que se para en el punto más alto de su trayectoria.
Está parado un instante (recuerda, parado significa con v=0) y vuelve a bajar "lo mismo que ha subido". Esto quiere decir que cuando va bajando, al pasar por cierta altura (la que sea) llevará la misma rapidez que llevaba cuando estaba subiendo. (Claro, si no hay aire, si no hay rozamiento)
¡Ojo, la misma velocidad no! porque en un caso se movía hacia arriba y en el otro hacia abajo. Pero sí la misma rapidez.
Actividad de Lectura
Las cosas son diferentes al MRU…
Una de las características del MRU era que se recorrían distancias iguales en tiempos iguales ¿lo recuerdas?
Como siempre que pensamos en un movimiento se nos viene a la cabeza un MRU, solemos pensar que esto es siempre así. Pero no, no es siempre así; en los MRUA no se recorren distancias iguales en tiempos iguales. En este ejemplo lo vas a comprobar.
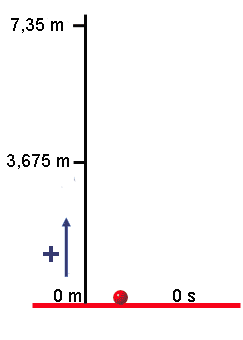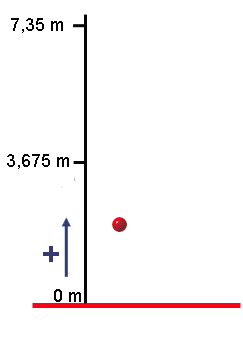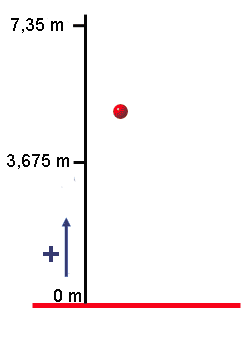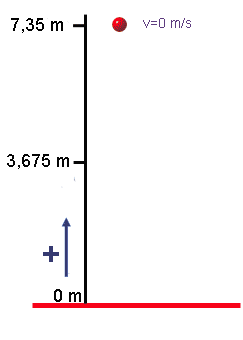
Volvamos al ejemplo de la pelota, pero ahora para preguntarnos en qué instante pasará la pelota justo por la mitad de su recorrido hacia arriba.
Podríamos pensar que si ha tardado 1,22 s en subir hasta 7,35 m... pues en subir hasta la mitad (3,675 m) deberá haber tardado también la mitad de tiempo, es decir, 0,61 s.
Pero... ¿Qué nos dirán los cálculos? ¿Estaremos en lo cierto?
En el ejemplo anterior ha habido que resolver algo nuevo, una ecuación de segundo grado con una incógnita.
Ya sabes que resolver ecuaciones es algo habitual en la Ciencia y la Tecnología, que, sin las Matemáticas, se quedarían sin su herramienta más preciada. Si no fuera por ellas, por las Matemáticas, no hubiera sido posible el espectacular desarrollo que la Ciencia y la Tecnología ha experimentado en los últimos siglos.
Ya viste cómo se resolvían las ecuaciones de primer grado. Eran fáciles ¿verdad? Pues bien, las de segundo grado, que son las que tienen la incógnita elevada al cuadrado, son aún más fáciles de resolver.
¡Solo hay que aplicar una fórmula!
Si haces clic aqui podrás ver cómo se ha resuelto la ecuación de segundo grado del ejemplo anterior.
Te sugerimos que no dejes de visitar el siguiente enlace. En él podrás aprender muchas cosas sobre las ecuaciones de segundo grado con una incógnita y practicar... ¡hasta que te hartes!
Objetivos
Para saber más…
¿Recuerdas que los sistemas de ecuaciones de primer grado con una incógnita se podían resolver gráficamente?
¿Se podrán resolver también así las ecuaciones de segundo grado?
Pues sí, las ecuaciones de segundo grado pueden resolverse gráficamente. Claro que, para ello, es necesario dibujar muy bien la parábola que representa a la función cuadrática y = ax2 + bx + c.
Las soluciones de la ecuación ax2 + bx + c = 0 son los puntos donde la parábola y = ax2 + bx + c corta al eje X
(Puedes practicar en la escena de más abajo... Si no puedes verla, prueba haciendo clic aquí)
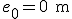 ;
; 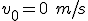 ;
; 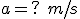
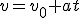 ;
; 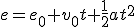
 ;
; 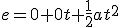
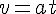 ;
; 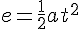
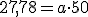 , lo que nos permite despejar la aceleración de esta sencilla ecuación de primer grado:
, lo que nos permite despejar la aceleración de esta sencilla ecuación de primer grado:
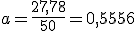
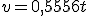
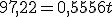 .
.
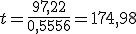
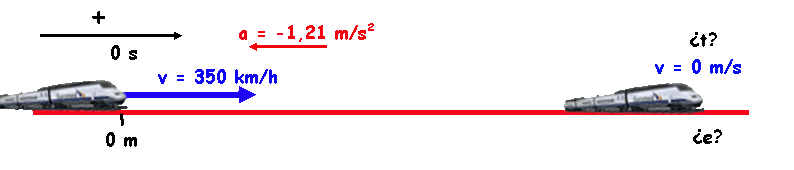
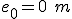 ;
; 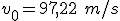 ;
; 
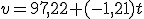 ;
; 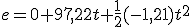
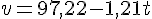 ;
; 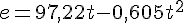
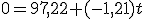 , una sencilla ecuación de primer grado de la que podemos despejar la t:
, una sencilla ecuación de primer grado de la que podemos despejar la t:
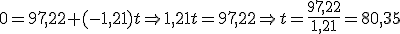
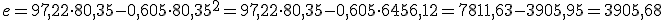
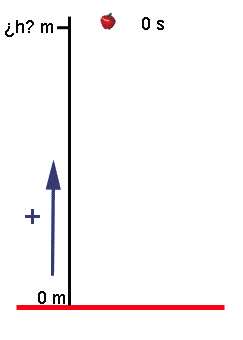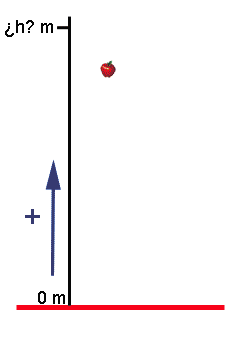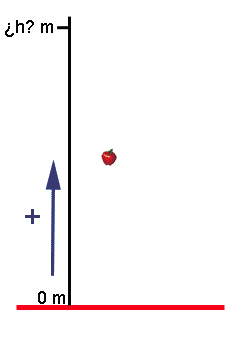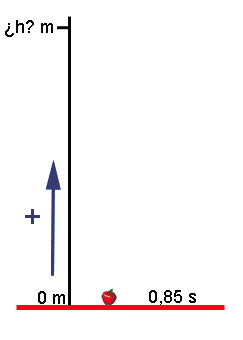
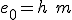 ¡No lo sabemos! Fíjate que es lo que queremos calcular, la altura desde la que cayó la manzana.
¡No lo sabemos! Fíjate que es lo que queremos calcular, la altura desde la que cayó la manzana.
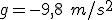 (la aceleración sí la sabemos, es la de la gravedad. Fíjate que, en el sistema de referencia que hemos elegido, es negativa, porque va hacia abajo, hacia el suelo)
(la aceleración sí la sabemos, es la de la gravedad. Fíjate que, en el sistema de referencia que hemos elegido, es negativa, porque va hacia abajo, hacia el suelo)
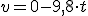 , que podemos escribir de modo más simple...
, que podemos escribir de modo más simple... 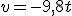
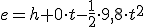 , que podemos escribir de modo más simple...
, que podemos escribir de modo más simple... 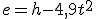
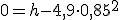
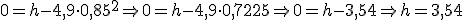
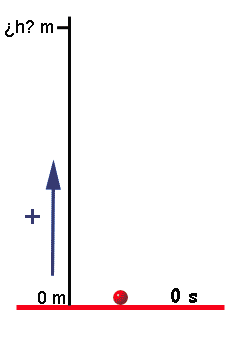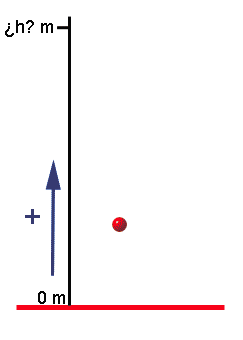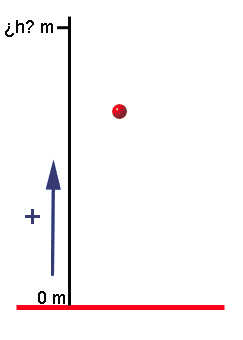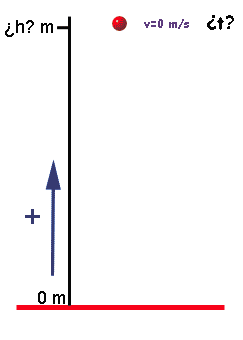
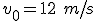 (positiva, pues va hacia arriba, en el sentido positivo del sistema de referencia)
(positiva, pues va hacia arriba, en el sentido positivo del sistema de referencia)
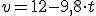 , que podemos escribir de modo más simple...
, que podemos escribir de modo más simple... 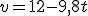
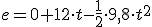 , que podemos escribir de modo más simple...
, que podemos escribir de modo más simple... 
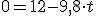 , obtenemos una sencilla ecuación de primer grado que nos permitirá obtener el tiempo que tarda la bola en subir:
, obtenemos una sencilla ecuación de primer grado que nos permitirá obtener el tiempo que tarda la bola en subir: