4. Energía potencial electrostática
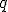 en un punto
del espacio, de acuerdo con la
Ley de Coulomb, al colocar otra carga
en un punto
del espacio, de acuerdo con la
Ley de Coulomb, al colocar otra carga  situada en una posición
situada en una posición 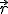 respecto de
respecto de 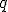 , experimentará una interacción electrostática de valor:
, experimentará una interacción electrostática de valor:
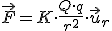
En el estudio que sigue se considerará la carga  fija y que la carga
fija y que la carga 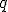 como móvil, de forma que puede desplazarse libremente en el espacio.
como móvil, de forma que puede desplazarse libremente en el espacio.
Actividad
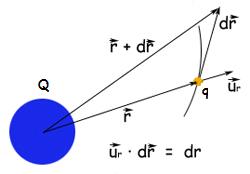 |
| Imagen 28. Elaboración propia |
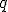 . Expresado de forma matemática:
. Expresado de forma matemática:
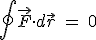
La demostración es análoga a la realizada para el campo gravitatorio:
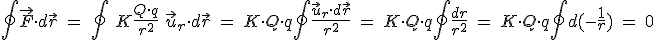
Por tanto, podemos definir una función
energía asociada a la posición que llamamos energía potencial electrostática, cuya diferencia
mide el trabajo de la fuerza electrostática cuando la carga 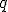 se desplaza de un
punto a otro.
se desplaza de un
punto a otro.
Una vez comprobado que se trata de una fuerza conservativa y la posibilidad de definir una energía potencial asociada, es sencillo encontrar su expresión. Para ello se calcula el trabajo que realiza la
fuerza electrostática en un desplazamiento de la carga de prueba 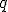 desde un punto
desde un punto 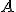 a otro
a otro 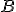 .
.
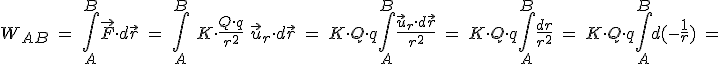
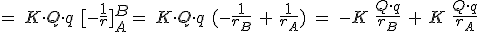
y recordando que el trabajo realizado por la fuerza se emplea en variar la energía potencial del sistema, es posible escribir:
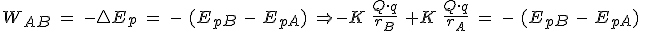
Tenemos definida la diferencia de energía
potencial electrostática entre dos puntos 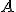 y
y 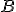 . Recuerda que si elegimos un origen de energía
potencial electrostática, podremos asociar con cada punto un valor de dicha
energía potencial.
. Recuerda que si elegimos un origen de energía
potencial electrostática, podremos asociar con cada punto un valor de dicha
energía potencial.
 |
| Imagen 29. Dzlot Creative commons |
El origen de energía potencial gravitatoria se toma normalmente en el infinito.
Con esta elección, desde el punto de vista físico, la energía potencial en un punto es
el trabajo realizado por la fuerza electrostática al trasladar la carga 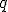 desde
dicho punto hasta el infinito, realizando todo el proceso a velocidad constante.
desde
dicho punto hasta el infinito, realizando todo el proceso a velocidad constante.
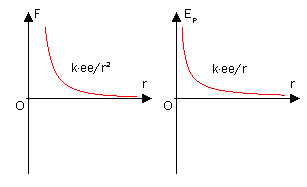
En la imagen puedes observar la representación gráfica de la fuerza y la energía potencial electrostática correspondiente a la interacción entre dos cargas positivas.
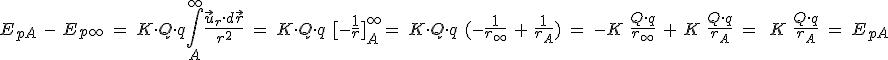
expresión correspondiente a la energía potencial electrostática en un punto.
Actividad
Tomando el origen de la energía potencial electrostática en el infinito, la energía potencial de la carga 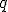 en un punto cualquiera será:
en un punto cualquiera será:
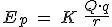
Así definida, la energía potencial electrostática de una carga eléctrica en un punto es igual al trabajo necesario para traer la carga desde el infinito hasta dicho punto.
A diferencia de lo que ocurría con el campo gravitatorio, el signo de la energía potencial depende del signo relativo de la carga del medio  y de la carga de prueba
y de la carga de prueba 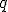 .
.
- Si ambas cargas tienen el mismo signo Ep será positiva y las fuerzas del campo no podrán realizar el proceso por ellas mismas, siendo necesario realizar un trabajo mediante una fuerza exterior, que se traducirá en un aumento de la energía potencial electrostática del sistema.
- Si las cargas tienen signo contrario Ep será negativa y el propio campo realizará el trabajo de traer la carga de prueba, disminuyendo en el proceso la energía potencial electrostática del sistema.
Ejemplo o ejercicio resuelto
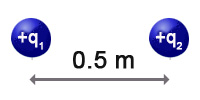 |
| Imagen 30. Elaboración propia |
Dos partículas con cargas q1 = 1 μC y q2 = 2 μC están separadas una distancia d = 0,5 m.
Calcula la fuerza que actúa sobre la segunda y su energía potencial electrostática.
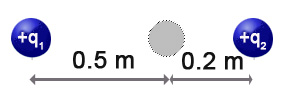 |
| Imagen 31. Elaboración propia |
AV - Pregunta Verdadero-Falso
Retroalimentación
Falso
Retroalimentación
Verdadero
La dependencia es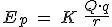
Retroalimentación
Verdadero
En la definición de energía potencial electrostática se ha tomado el origen en el infinito, por lo que allí toma el valor nulo.