2.3. Proporcionalidad inversa
Al químico y filósofo irlandés del siglo XVII, Boyle, se debe la ley que lleva su nombre: "si un gas se mantiene a temperatura constante, su volumen es inversamente proporcional a la presión".
En el siguiente vídeo podemos disfrutar de una justificación casera de dicha ley:
Lo que Boyle quiso decir es que la relación que existe entre el volumen 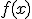 , expresado en litros, y la presión
, expresado en litros, y la presión 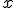 , expresada en Newton por cm2, viene dada por la función:
, expresada en Newton por cm2, viene dada por la función: 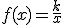 , donde
, donde 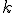 es una constante.
es una constante.
El famoso matemático griego Arquímedes dijo aquella famosa frase de "dadme un punto de apoyo y moveré el mundo". Si consideramos 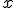 la distancia en metros al punto de apoyo, y
la distancia en metros al punto de apoyo, y 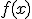 la fuerza medida en Newton que necesito aplicar para levantar un cuerpo de
la fuerza medida en Newton que necesito aplicar para levantar un cuerpo de 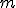 kilogramos de masa, lo dicho por Arquímedes se puede expresar como
kilogramos de masa, lo dicho por Arquímedes se puede expresar como 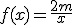 .
.
Observa que las dos funciones tienen expresiones similares, un número divido entre x. A este tipo de funciones se las denomina de proporcionalidad inversa. El calificativo de inversa está muy bien puesto, en ambos casos, si 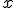 es pequeño, cercano a 0,
es pequeño, cercano a 0, 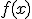 es grande. Y viceversa, si
es grande. Y viceversa, si 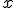 es grande,
es grande, 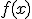 se hace pequeño.
se hace pequeño.
Como acabamos de ver, son buenas para modelizar muchos procesos físicos de la naturaleza. Pero también se ajustan muy bien a otros tipos de problemas, como pueden ser los de reparto.
3
 |
| Fotografía en Flickr por TonioMora bajo CC |
Las bombillas que se utilizan en las torres de iluminación de los conciertos son de gran potencia, frágiles y además caras. Las empresas de material eléctrico cobran 240 euros por el transporte más 300 euros por bombilla.
Vamos a estudiar el coste de una bombilla en función de la cantidad de bombillas que se van a comprar.
Consideramos la función  , que asocia al número de bombillas que se encargan,
, que asocia al número de bombillas que se encargan, 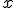 , el coste individual que tendrá que pagar por cada una de ellas,
, el coste individual que tendrá que pagar por cada una de ellas, 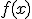 .
.
Te pedimos que representes gráficamente y determines la expresión analítica de la función  .
.
¿Crees que existirá un precio mínimo a pagar por bombilla si aumentara enormemente la cantidad de bombillas compradas? Razona tus respuestas.
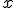 , número de bombillas compradas , número de bombillas compradas
|
1 | 2 | 3 | 4 | 10 | 100 | 200 |
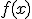 , precio individual a pagar por cada bombilla , precio individual a pagar por cada bombilla |
La función del ejercicio anterior también es de proporcionalidad inversa. Están funciones tienen una gráfica muy característica. Observa que si el número de bombillas que se compra es pequeño, el coste unitario por cada una de ellas es grande, en tanto que si se encargan un gran número de bombillas, dicho coste va disminuyendo.
¿Hasta dónde disminuye? Supongamos que encargan 1.000 bombillas, 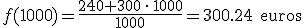 . Si haces la misma operación para 10.000, 100.000 bombillas, podrás ver que el precio unitario no baja de 300 euros, se aproxima a esa cantidad, pero sin bajar de ella. Se dice que
. Si haces la misma operación para 10.000, 100.000 bombillas, podrás ver que el precio unitario no baja de 300 euros, se aproxima a esa cantidad, pero sin bajar de ella. Se dice que 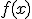 tiene una asíntota en la recta
tiene una asíntota en la recta 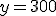 .
.
Y esa es otra de las características de las funciones de proporcionalidad inversa.
Importante
A las funciones cuya expresión algebraica es del tipo 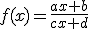 donde
donde  ,
, 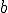 ,
,  y
y 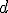 son números reales y
son números reales y  , se les denomina funciones de proporcionalidad inversa.
, se les denomina funciones de proporcionalidad inversa.
 |
| Imagen de elaboración propia |
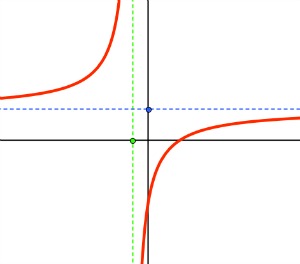
En la imagen de la derecha aparece representada 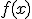 . Su gráfica es una hipérbola equilátera. Las siluetas de todas las funciones de proporcionalidad inversa (PI) son muy similares. Pueden estar desplazadas, ser más o menos abiertas, crecer o decrecer, en función de los parámetros
. Su gráfica es una hipérbola equilátera. Las siluetas de todas las funciones de proporcionalidad inversa (PI) son muy similares. Pueden estar desplazadas, ser más o menos abiertas, crecer o decrecer, en función de los parámetros  ,
, 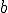 ,
,  y
y 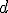 .
.
El dominio de las funciones PI es todo 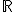 menos el número donde se anula el denominador, es decir donde
menos el número donde se anula el denominador, es decir donde 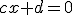 . Si resolvemos esa ecuación de primer grado, ese número es
. Si resolvemos esa ecuación de primer grado, ese número es 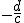 . En la gráfica, el punto verde que se encuentra en el eje OX, tiene coordenadas
. En la gráfica, el punto verde que se encuentra en el eje OX, tiene coordenadas 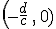 . En dicho punto la función tiene una asíntota vertical de ecuación
. En dicho punto la función tiene una asíntota vertical de ecuación 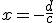 , que es la recta verde.
, que es la recta verde.
El recorrido de las funciones PI es todo 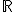 menos el punto
menos el punto 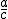 . En la gráfica, el punto azul, que pertenece al eje OY, tiene de coordenadas
. En la gráfica, el punto azul, que pertenece al eje OY, tiene de coordenadas  . En él la función tiene una asíntota horizontal, que corresponde a la recta azul de ecuación
. En él la función tiene una asíntota horizontal, que corresponde a la recta azul de ecuación 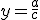 .
.
Como se puede ver, las asíntotas son rectas que se aproximan a la función, que en cierto sentido, moldean su gráfica.
En el caso del precio de las bombillas, la asíntota vertical sería 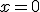 , dado que 0 es el número que anula el denominador. En tanto que la asíntota horizontal sería
, dado que 0 es el número que anula el denominador. En tanto que la asíntota horizontal sería 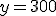 , ya que
, ya que 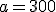 y
y 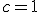 .
.
En la siguiente vídeo se explica con detalle cómo condiciona a la gráfica de una función el hecho de tener asíntotas:
Para practicar con las funciones de proporcionalidad inversa te puedes guiar por la ruta que te marca la escena de GeoGebra a la que podrás acceder si haces clic en la siguiente imagen. Es conveniente que representes tú las funciones que se proponen y que compruebes con la escena si son correctos los pasos que vas dando.
 |
Caso de estudio
Estudia y representa la función racional: