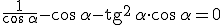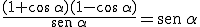2.5 Identidades y ecuaciones trigonométricas sencillas.

Por último y aprovechando toda la teoría explicada en los apartados anteriores vamos a aplicarla en dos tipos de ejercicios muy usuales en trigonometría,demostración de identidades y resolución de ecuaciones.

 

Identidades trigonométricas

Para explicar en qué consisten vamos a demostrar el siguiente ejemplo:

 

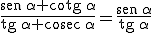
\frac{\begin{verbatim}sen\end{verbatim}\, \alpha + \begin{verbatim}cotg\end{verbatim}\, \alpha}{ \begin{verbatim}tg\end{verbatim}\, \alpha + \begin{verbatim}cosec\end{verbatim}\, \alpha}= \frac{\begin{verbatim}sen\end{verbatim}\, \alpha}{ \begin{verbatim}tg\end{verbatim}\, \alpha}

 

Para demostrar una identidad de este tipo empezamos desarrollando uno de los términos de la igualdad intentando llegar mediante una cadena de igualdades al otro término. Si esto no es posible desarrollaríamos también el otro término y debermos llegar a la misma expresión que en el anterior.

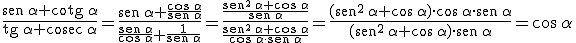
\frac{\begin{verbatim}sen\end{verbatim}\, \alpha + \begin{verbatim}cotg\end{verbatim}\, \alpha}{ \begin{verbatim}tg\end{verbatim}\, \alpha + \begin{verbatim}cosec\end{verbatim}\, \alpha} =\frac{\begin{verbatim}sen\end{verbatim}\, \alpha + \frac{\cos\, \alpha}{\begin{verbatim}sen\end{verbatim}\, \alpha}}{ \frac{\begin{verbatim}sen\end{verbatim}\, \alpha }{\cos\, \alpha }+ \frac{1}{\begin{verbatim}sen\end{verbatim}\, \alpha}} =\frac{\frac{\begin{verbatim}sen\end{verbatim}^2\, \alpha + \cos\, \alpha}{\begin{verbatim}sen\end{verbatim}\, \alpha}}{ \frac{\begin{verbatim}sen\end{verbatim}^2\, \alpha +\cos\, \alpha }{ \cos \, \alpha \cdot \begin{verbatim}sen\end{verbatim}\, \alpha }} =\frac{(\begin{verbatim}sen\end{verbatim}^2\, \alpha + \cos\, \alpha) \cdot \cos \, \alpha \cdot \begin{verbatim}sen\end{verbatim}\, \alpha }{ (\begin{verbatim}sen\end{verbatim}^2\, \alpha +\cos\, \alpha) \cdot \begin{verbatim}sen\end{verbatim}\, \alpha } = \cos \, \alpha

En primer lugar elegimos el término con más miembros y empezamos a desarrollar:

Como sabemos que 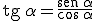\begin{verbatim}tg\end{verbatim} \, \alpha=\frac{\begin{verbatim}sen\end{verbatim}\, \alpha}{\cos \, \alpha} despejando 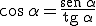\cos \, \alpha=\frac{\begin{verbatim}sen\end{verbatim}\, \alpha}{\begin{verbatim}tg\end{verbatim} \, \alpha} como queríamos demostrar.

Ecuaciones trigonométricas

Empecemos resolviendo una ecuación trigonométrica sencilla, por ejemplo 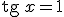\begin{verbatim}tg\end{verbatim} \, x=1

En primer lugar tenemos que determinar en qué cuadrante se encuentran las posibles soluciones. Como la tangente que nos dan es positiva podemos considerar que los ángulos que buscamos son ángulos del primer y tercer cuadrante. Determinar el ángulo del primer cuadrante es inmediato porque se corresponde con la tangente de una ángulo que conocemos, es decir, que la primera solución a la que nos referimos es x=45º.

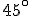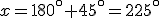El ángulo del tercer cuadrante con el que se relaciona 45^\circ, por lo visto en un apartado anterior, seria x=180^\circ+45^\circ=225^\circ.

Nos podríamos preguntar ¿serían éstas dos las únicas soluciones? No. Hay que tener en cuenta que si damos vueltas completas a la circunferencia obtenemos soluciones nuevas. Para expresar esto diríamos que las soluciones serían:

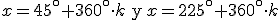
x=45^\circ+360^\circ \cdot k \begin{verbatim} y \end{verbatim} x=225^\circ+360^\circ \cdot

donde k representa cualquier valor número entero (algebraicamente esto se expresa).

Pero este caso sería especial porque si nos damos cuenta como 225º=180º+45º y 180º supone un arco que abarca media circunferencia tenemos que podemos expresar las soluciones de esta ecuación como

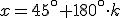
x=45^\circ+180^\circ \cdot k

siendo 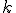k cualquier número entero.

Resolvamos ahora una ecuación un poco más compleja:

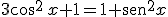
3\cos^2 \, x+ 1= 1 + \begin{verbatim}sen\end{verbatim}^2 x

Para dejar todo con una única razón trigonométrica podemos expresar 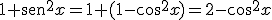1+\begin{verbatim}sen\end{verbatim}^2x=1+(1-cos^2x)=2-cos^2x y de esta forma la ecuación solo dependería del \cos \, x: 

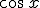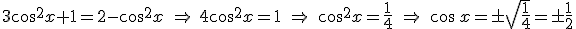
3 \cos^2 x + 1 = 2 - \cos ^2 x \ \Rightarrow \ 4 \cos^2 x = 1 \ \Rightarrow \ \cos^2 x = \frac{1}{4} \ \Rightarrow \ \cos \, x= \pm\sqrt{\frac{1}{4}}= \pm \frac{1}{2}

Al tener dos soluciones una positiva y otra negativa significa que hay una solución diferente en cada cuadrante. Primero determinar que el ángulo del cuadrante que tiene este coseno es 60º. A partir de este ángulo determinamos el resto de soluciones.

En el segundo cuadrante sería x=180º-60º=120º, en el tercero x=180º+60º=240º y en el cuarto x=360º-60º=300º. Por tanto, podemos decir que las soluciones son:

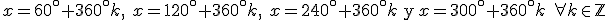x=60^\circ+360^\circ k, \ x= 120^\circ +360^\circ k, \ x=240^\circ+360^\circ k \begin{verbatim} y \end{verbatim} x=300^\circ+360^\circ k \ \forall k \in \mathbb{Z} .

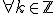De forma equivalente, podríamos simplificar y nos quedarían las soluciones:

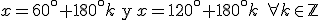
x=60^\circ+180^\circ k \begin{verbatim} y \end{verbatim} x=120^\circ+180^\circ k \ \forall k \in \mathbb{Z}

Reflexión

Demuestra las siguientes identidades:

  • \frac{1}{\cos \, \alpha}- \cos \, \alpha -\begin{verbatim}tg\end{verbatim}^2 \, \alpha \cdot \cos \, \alpha =0

  • \frac{(1 + \cos \, \alpha)(1 - \cos \, \alpha)} {\begin{verbatim}sen\end{verbatim} \, \alpha} = \begin{verbatim}sen\end{verbatim} \, \alpha

Reflexión

Resuelve la ecuación

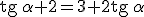
\begin{verbatim}tg\end{verbatim} \, \alpha +2 = 3+2 \begin{verbatim}tg\end{verbatim} \, \alpha