2.2. Relaciones fundamentales entre las razones trigonométricas de un mismo ángulo

Importante

De las definiciones del apartado anterior se pueden deducir varias relaciones fundamentales entre las razones trigonométricas de un mismo ángulo:

$\begin{verbatim}tg \end{verbatim}\alpha=\frac{\begin{verbatim}sen \end{verbatim}\alpha}{\cos \ \alpha}$

$\begin{verbatim}sen\end{verbatim}^2 \alpha + \cos^2 \alpha =1$

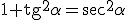
$1+\begin{verbatim}tg\end{verbatim}^2\alpha =\begin{verbatim}sec\end{verbatim}^2\alpha$

Veamos sus demostraciones:

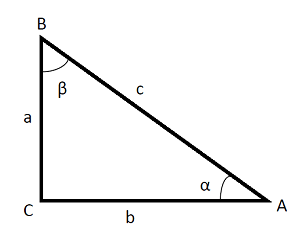
$\begin{verbatim}tg \end{verbatim}\alpha=\frac{\begin{verbatim}sen \end{verbatim}\alpha}{\cos \ \alpha}$

Teniendo en cuenta el dibujo y las definiciones de seno y de coseno de un ángulo deducimos que:

$\frac{\begin{verbatim}sen \end{verbatim}\alpha}{\cos \ \alpha} = \frac{\frac{a}{c}}{\frac{b}{c}} = \frac{a \cdot c}{b \cdot c} = \begin{verbatim}tg \end{verbatim}\alpha$

$\begin{verbatim}sen\end{verbatim}^2 \alpha + \cos^2 \alpha =1$

$\begin{verbatim}sen\end{verbatim}^2 \alpha + \cos^2 \alpha = \left( \frac{a}{c} \right)^2 + \left( \frac{b}{c} \right)^2 = \frac{a^2}{c^2} + \frac{b^2}{c^2} = \frac{a^2+b^2}{c^2} = \frac{c^2}{c^2} =1$

Como estamos trabajando con un triángulo rectángulo se cumple el teorema de Pitágoras de manera que a^2+b^2=c^2

$1+\begin{verbatim}tg\end{verbatim}^2\alpha =\begin{verbatim}sec\end{verbatim}^2\alpha$

$1+\begin{verbatim}tg\end{verbatim}^2\alpha = 1+ \left( \frac{\begin{verbatim}sen \end{verbatim} \alpha}{\cos \ \alpha} \right)^2 = 1+ \frac{\begin{verbatim}sen\end{verbatim}^2 \alpha}{\cos^2 \alpha} = \frac{\cos^2 \alpha + \begin{verbatim}sen\end{verbatim}^2 \alpha}{\cos^2 \alpha} = \frac{1}{\cos^2 \alpha} = \left( \frac{1}{\cos \ \alpha} \right)^2 = \left(\begin{verbatim}sec \end{verbatim} \alpha \right)^2 = \begin{verbatim}sec\end{verbatim}^2 \alpha$

Veamos un ejemplo de cómo poder utilizar estas relaciones:

Supongamos que conocemos una de las razones trigonométricas de un ángulo agudo desconocido y que queremos averiguar el resto, por ejemplo:

$\cos \ \alpha=\frac{3}{5}$

Como sabemos que:

$\begin{verbatim}sen\end{verbatim}^2 \alpha + \cos^2 \alpha =1$

Sustituyendo en esta expresión y después despejando obtenemos:

$\begin{verbatim}sen\end{verbatim}^2 \alpha + \left(\frac{3}{5}\right)^2= 1 \ \Rightarrow \ \begin{verbatim}sen\end{verbatim}^2 \alpha +\frac{9}{25}=1 \ \Rightarrow \ \begin{verbatim}sen\end{verbatim}^2 \alpha=1-\frac{9}{25} \ \Rightarrow \ \begin{verbatim}sen\end{verbatim}^2 \alpha =\frac{16}{25} \ \Rightarrow \ \begin{verbatim}sen \end{verbatim} \alpha = \pm \sqrt{\frac{16}{25}}=\pm \frac{4}{5}$

Si descartamos la raiz negativa por ser un ángulo agudo tenemos que:

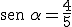
$\begin{verbatim}sen \end{verbatim}\alpha =\frac{4}{5}$

También hemos demostrado que:

$\begin{verbatim}tg \end{verbatim}\alpha=\frac{\begin{verbatim}sen \end{verbatim}\alpha}{\cos \ \alpha}$

Por tanto,

$\begin{verbatim}tg \end{verbatim}\alpha =\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{4}{3}$

y las razones trigonométricas inversas:

$\begin{verbatim}cosec \end{verbatim}\alpha =\frac{1}{\begin{verbatim}sen \end{verbatim}\alpha }=\frac{1}{\frac{4}{5}} =\frac{5}{4}$

$\begin{verbatim}sec \end{verbatim}\alpha =\frac{1}{\cos \ \alpha }=\frac{1}{\frac{3}{5}} =\frac{5}{3}$

$\begin{verbatim}cotg \end{verbatim}\alpha =\frac{1}{\begin{verbatim}tg \end{verbatim}\alpha }=\frac{1}{\frac{4}{3}} =\frac{3}{4}$

Reflexión

Determina el resto de razones trigonométricas del ángulo 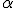$\alpha$ si conocemos que

$\begin{verbatim}cosec \end{verbatim} \alpha = \frac{13}{5}$

Reflexión

Calcula las razones trigonométricas que faltan teniendo en cuenta que:

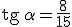
$\begin{verbatim}tg \end{verbatim}\alpha = \frac{8}{15}$

Pregunta Verdadero-Falso

Determina si las afirmaciones son verdaderas o falsas

Retroalimentación

Falso

Nunca el coseno puede ser mayor que uno puesto que si así fuese al elevarlo al cuadrado también sería un número mayor que uno y al sumarle el valor del seno al cuadrado quedaría un número mayor que uno y por la identidad trigonométrica que acabamos de demostrar esto es imposible.

Retroalimentación

Verdadero

Como la tangente se calcula dividiendo el seno entre el coseno si el valor del seno que es el que se pone en el numerador es mayor que el del coseno la división saldrá mayor que uno.

2.2. Relaciones fundamentales entre las razones trigonométricas de un mismo ángulo

Importante

Reflexión

Retroalimentación

Reflexión

Retroalimentación

Pregunta Verdadero-Falso

Pregunta 1

Retroalimentación

Pregunta 2

Retroalimentación